Question

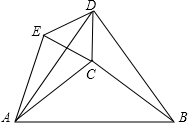如图，在等腰Rt△ABC中，AC=BC，以斜边AB为一边作等边△ABD，使点C，D在AB的同侧；再以CD为一边作等边△CDE，使点C，E落在AD的异侧．若AE=1，则CD的长为（　　）

• A、

  3

  -1
• B、

  3 -1

  2

• C、

  6

  -

  2

• D、

  6 - 2

  2

Answer 1

分析：在延长DC后，欲求DC，即DF-CF．而DF是直角三角形ADF的高，CF是等腰直角三角形ABC斜边上的高，根据题中条件，求出二者即可．

解答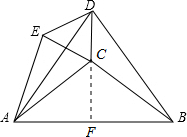：解：延长DC交AB于F
由题意易得，
∵AC=BC，
∴C在AB的垂直平分线上，
同理，D在AB的垂直平分线上，
∴CD是等边三角形ABD的角平分线，
所以∠ADC=30°，
则∠EDA=60°-30°=30°，
∵ED=DC，AD=AD，∠EDA=∠CDA=30°
∴△EDA≌△CDA
∴EA=AC=1
∴在等腰Rt△ABC中AB=

2

∴BF=CF=

2

2

，
在△ABD中tan∠BDF=tan30°=

BF

DF

，
∴DF=

6

2

，
∴DC=DF-CF=

6 - 2

2

．
故选D．

点评：此题主要考查了等腰三角形、等边三角形和直角三角形的性质，综合利用了勾股定理和全等三角形的判定．