题目内容
【题目】给下面命题的说理过程填写依据.
已知:如图,直线AB,CD相交于点O,EO⊥CD,垂足为O,OF平分∠BOD,对∠EOF=![]() ∠BOC说明理由.
∠BOC说明理由.
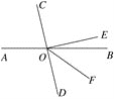
理由:因为∠AOC=∠BOD( ),
∠BOF=![]() ∠BOD( ),
∠BOD( ),
所以∠BOF=![]() ∠AOC( ).
∠AOC( ).
因为∠AOC=180°-∠BOC( ),
所以∠BOF=90°-![]() ∠BOC.
∠BOC.
因为EO⊥CD( ),
所以∠COE=90°( )
因为∠BOE+∠COE=∠BOC( ),
所以∠BOE=∠BOC-∠COE.
所以∠BOE=∠BOC-90°( )
因为∠EOF=∠BOE+∠BOF( )
所以∠EOF=(∠BOC-90°)+(90°![]() ∠BOC)( )
∠BOC)( )
所以∠EOF=![]() ∠BOC.
∠BOC.
【答案】对顶角相等,角平分线的定义,等量代换,平角的定义,已知,垂直的定义,两角和的定义,等量代换,两角和的定义,等量代换.
【解析】
根据对顶角的性质得到∠AOC=∠BOD,由角平分线的定义得到∠BOF=![]() ∠BOD,等量代换得到∠BOF=
∠BOD,等量代换得到∠BOF=![]() ∠AOC,由垂直的定义得到∠COE=90°,等量代换得到∠BOE=∠BOC-90°,于是得到结论.
∠AOC,由垂直的定义得到∠COE=90°,等量代换得到∠BOE=∠BOC-90°,于是得到结论.
解:因为∠AOC=∠BOD(对顶角相等),∠BOF=![]() ∠BOD(平分线的定义),
∠BOD(平分线的定义),
所以∠BOF=![]() ∠AOC(等量代换).
∠AOC(等量代换).
因为∠AOC=180°-∠BOC(平角的定义),所以∠BOF=90°-![]() ∠BOC.
∠BOC.
因为EO⊥CD(已知),所以∠COE=90°(垂直的定义)
因为∠BOE+∠COE=∠BOC(两角和的定义),
所以∠BOE=∠BOC-∠COE.
所以∠BOE=∠BOC-90°(等量代换)
因为∠EOF=∠BOE+∠BOF(两角和的定义)
所以∠EOF=(∠BOC-90°)+(90°![]() ∠BOC)(等量代换)
∠BOC)(等量代换)
所以∠EOF=![]() ∠BOC.
∠BOC.
故答案为:对顶角相等,角平分线的定义,等量代换,平角的定义,已知,垂直的定义,两角和的定义,等量代换,两角和的定义,等量代换.

 作业辅导系列答案
作业辅导系列答案