题目内容
某校九（1）、九（2）两班的班长交流了为四川安雅地震灾区捐款的情况：
（Ⅰ）九（1）班班长说：“我们班捐款总数为1200元，我们班人数比你们班多8人．”
（Ⅱ）九（2）班班长说：“我们班捐款总数也为1200元，我们班人均捐款比你们班人均捐款多20%．”
请根据两个班长的对话，求这两个班级每班的人均捐款数．
解：设九（1）班的人均捐款数为x元，则九（2）班的人均捐款数为（1+20%）x元，
则：
-
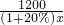=8，
解得：x=25，
经检验，x=25是原方程的解．
九（2）班的人均捐款数为：（1+20%）x=30（元）
答：九（1）班人均捐款为25元，九（2）班人均捐款为30元．
分析：首先设九（1）班的人均捐款数为x元，则九（2）班的人均捐款数为（1+20%）x元，然后根据九（1）班人数比九（2）班多8人，即可得方程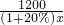：-=8，解此方程即可求得答案．
点评：本题考查分式方程的应用．注意分析题意，找到合适的等量关系是解决问题的关键．
则：
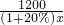-=8，解得：x=25，
经检验，x=25是原方程的解．
九（2）班的人均捐款数为：（1+20%）x=30（元）
答：九（1）班人均捐款为25元，九（2）班人均捐款为30元．
分析：首先设九（1）班的人均捐款数为x元，则九（2）班的人均捐款数为（1+20%）x元，然后根据九（1）班人数比九（2）班多8人，即可得方程：
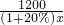-=8，解此方程即可求得答案．点评：本题考查分式方程的应用．注意分析题意，找到合适的等量关系是解决问题的关键．
练习册系列答案
相关题目
某山区有23名中小学生因贫困失学需要捐助，资助一名中学生需要学习费用a元，资助一名小学生需要学习费用b元，某校学生积极捐款，初中各年级学生捐款数额与用其恰好能帮助的贫困中学生和小学生人数的部分情况如下表：
（1）求a、b的值；
（2）九年级学生的捐款解决了其余贫困中小学生的学习费用，请将九年级学生可捐助的贫困中、小学生人数直接填入上表中（不需要写出计算过程）．
| 七年级 | 八年级 | 九年级 | |
| 捐款数额（元） | 4000 | 4200 | 7400 |
| 捐助贫困中学生（名） | 2 | 3 | |
| 捐助贫困小学生（名） | 4 | 3 |
（2）九年级学生的捐款解决了其余贫困中小学生的学习费用，请将九年级学生可捐助的贫困中、小学生人数直接填入上表中（不需要写出计算过程）．
