题目内容
点M（x，y）可以在数-1，0，1，2中任意选取．试求：
（1）点M在第二象限内的概率；
（2）点M在直线y=-2x+3上的概率．
（1）点M在第二象限内的概率；
（2）点M在直线y=-2x+3上的概率．
分析：列表得出所有等可能的情况数，
（1）找出M在第二象限的情况数，即可求出所求的概率；
（2）找出M在直线y=-2x+3上的情况数，即可求出所求的概率．
（1）找出M在第二象限的情况数，即可求出所求的概率；
（2）找出M在直线y=-2x+3上的情况数，即可求出所求的概率．
解答：解：点M的坐标情况列表表示如下：
通过列表分析知所有可能的点有16（种），
（1）在第二象限内的点有2个，即（-1，1），（-1，2）
∴P（在第二象限内的点）=
=
；
（2）在直线y=2x+3上的点有两个，即（1，1），（2，-1）
∴P（在直线y=-2x+3上的点）=
=
．
x y |
-1 | 0 | 1 | 2 |
| -1 | （-1，-1） | （-1，0） | （-1，1） | （-1，2） |
| 0 | （0，-1） | （0，0） | （0，1） | （0，2） |
| 1 | （1，-1） | （1，0） | （1，1） | （1，2） |
| 2 | （2，-1） | （2，0） | （2，1） | （2，2） |
（1）在第二象限内的点有2个，即（-1，1），（-1，2）
∴P（在第二象限内的点）=
| 2 |
| 16 |
| 1 |
| 8 |
（2）在直线y=2x+3上的点有两个，即（1，1），（2，-1）
∴P（在直线y=-2x+3上的点）=
| 2 |
| 16 |
| 1 |
| 8 |
点评：此题考查了列表法与树状图法，点的坐标，以及一次函数图象上点的特征，用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
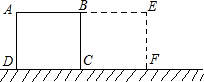已知正方形纸片ABCD的边长AB=2cm，把正方形ABCD绕某一点按顺时针方向旋转，使它旋转后能与正方形BEFC重合．
52、如图所示，在菱形ABCD中，AB=10，∠BAD=60°，点M从点A以每秒1个单位长度的速度沿着AD边向点D移动，设点M移动的时间为t（0≤t≤10），点N为BC边上任意一点，在点M移动的过程中，线段MN是否可以将菱形ABCD分割成面积相等的两部分？请说明理由．