题目内容
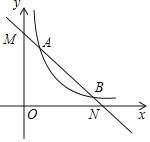
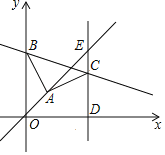
【题目】如图,平面直角坐标系中,![]() ,
,![]() 为
为![]() 轴正半轴上一点,连接
轴正半轴上一点,连接![]() ,在第一象限作
,在第一象限作![]() ,
,![]() ,过点
,过点![]() 作直线
作直线![]() 轴于
轴于![]() ,直线
,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,且
,且![]() ,则直线
,则直线![]() 解析式为____________.
解析式为____________.
【答案】![]()
【解析】
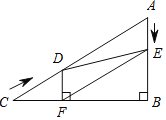
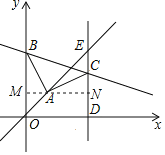
过A作AM⊥y轴,交y轴于M,交CD于N,根据∠BMA=∠ANC=90°,∠BAC=90°可以得到∠ABM=∠CAN,再根据A点坐标可以得出OM=DN=AM=4,求出△ABM≌△CAN,根据全等的性质求出AN=BM,CN=4,再根据ED=5EC和E在直线y=x上求出E的坐标,即可求出MN=10,CD=8,AN=BM=MN-AM=6的值,得出C(10,8),B(0,10)代入y=kx+b中,即可求出.
解:过![]() 作
作![]() 轴,交
轴,交![]() 轴于
轴于![]() ,交
,交![]() 于
于![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,
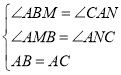 ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() 设
设![]() ,
,![]() ,
,
![]() ,
,
![]() 点
点![]() 在直线
在直线![]() 上,
上,
![]() ,
,
则![]() ,
,
![]() ,即
,即![]() ,
,![]() .
.
![]() 点
点![]() 在直线
在直线![]() 上,
上,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
设直线![]() 的解析式是
的解析式是![]() ,
,
把![]() 代入得:
代入得:![]() ,
,
即直线![]() 的解析式是
的解析式是![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目