题目内容
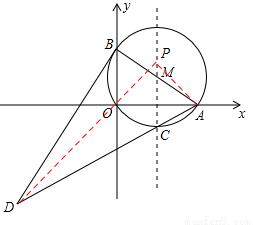
如图,在平面直角坐标系中,⊙M过原点O,与x轴交于A(4,0),与y轴交于B(0,3),点C为劣弧AO的中点,连接AC并延长到D,使DC=4CA,连接BD.
(1)求⊙M的半径;
(2)证明:BD为⊙M的切线;
(3)在直线MC上找一点P,使|DP﹣AP|最大.

(1)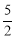 ;(2)证明见解析;(3)取点A关于直线MC的对称点O,连接DO并延长交直线MC于P,此P点为所求,且线段DO的长为|DP﹣AP|的最大值,为
;(2)证明见解析;(3)取点A关于直线MC的对称点O,连接DO并延长交直线MC于P,此P点为所求,且线段DO的长为|DP﹣AP|的最大值,为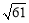 .
.
【解析】
试题分析:(1)利用A,B点坐标得出AO,BO的长,进而得出AB的长,即可得出圆的半径.
(2)根据B,D 两点求出直线BD表达式,求出BD与与 x 轴交点Q的坐标,从而求出AB,QA,BQ的长,根据勾股定理逆定理得出BD⊥AB,求出BD为⊙M的切线.
(3)取点A关于直线MC的对称点O,连接DO并延长交直线MC于P,此P点为所求,且线段DO的长为|DP﹣AP|的最大值.根据D,O两点求出直线DO表达式为y=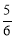 x, 又在直线 DO 上的点P的横坐标为2,所以 p(2,
x, 又在直线 DO 上的点P的横坐标为2,所以 p(2,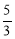 ),此时|DP﹣AP|=DO=
),此时|DP﹣AP|=DO=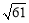 .
.
试题解析:【解析】
(1)∵由题意可得出:OA2+OB2=AB2,AO=4,BO=3,∴AB=5.∴圆的半径为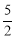 .
.
(2)证明:由题意可得出:M(2,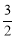 ).
).
∵C为劣弧AO的中点,由垂径定理且 MC=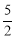 ,故 C(2,﹣1).
,故 C(2,﹣1).
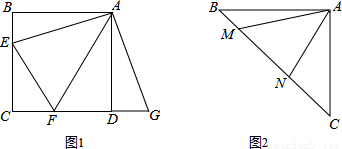
如答图1,过 D 作 DH⊥x 轴于 H,设 MC 与 x 轴交于 N,
则△ACN∽△ADH,
又∵DC=4AC,∴ DH=5NC=5,HA=5NA=10.∴D(﹣6,﹣5).
设直线BD表达式为:y=ax+b,
则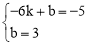 ,解得:
,解得: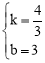 .∴直线BD表达式为:y=
.∴直线BD表达式为:y=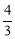 x+3.
x+3.
设 BD 与 x 轴交于Q,则Q(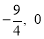 ).∴OQ=
).∴OQ=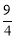 .∴
.∴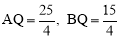 .
.
∵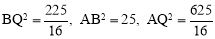 ,∴
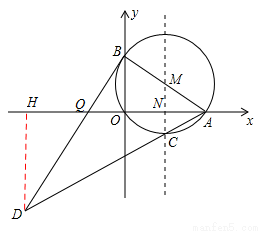
,∴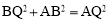 .∴△ABQ是直角三角形,即∠ABQ=90°.
.∴△ABQ是直角三角形,即∠ABQ=90°.
∴BD⊥AB,BD为⊙M的切线.
(3)如答图2,取点A关于直线MC的对称点O,连接DO并延长交直线MC于P,此P点为所求,且线段DO的长为|DP﹣AP|的最大值.
设直线DO表达式为 y=kx,
∴﹣5=﹣6k,解得:k=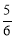 .
.
∴直线DO表达式为 y=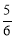 x
x
又∵在直线DO上的点P的横坐标为2,∴y=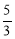 .∴P(2,
.∴P(2,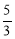 ).此时|DP﹣AP|=DO=
).此时|DP﹣AP|=DO=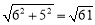 .
.
考点:1.圆的综合题;2.勾股定理和逆定理;3.垂径定理;4.相似三角形的判定和性质;5.待定系数法的应用;6.直线上点的坐标与方程的关系;7.切线的判定;8.轴对称的应用(最短线路问题).

 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案在一次科技知识竞赛中,两组学生成绩统计如下表,通过计算可知两组的方差为 ,
, .下列说法:
.下列说法:
①两组的平均数相同;
②甲组学生成绩比乙组学生成绩稳定;
③甲组成绩的众数>乙组成绩的众数;
④两组成绩的中位数均为80,但成绩≥80的人数甲组比乙组多,从中位数来看,甲组成绩总体比乙组好;⑤成绩高于或等于90分的人数乙组比甲组多,高分段乙组成绩比甲组好.
其中正确的共有( )
分数 | 50 | 60 | 70 | 80 | 90 | 100 | |
人数 | 甲组 | 2 | 5 | 10 | 13 | 14 | 6 |
乙组 | 4 | 4 | 16 | 2 | 12 | 12 | |
(A)2种 (B)3种 (C)4种 (D)5种
 的大致图象如图所示,关于该二次函数,下列说法错误的是( )
的大致图象如图所示,关于该二次函数,下列说法错误的是( )

 ,y随x的增大而减小
,y随x的增大而减小 ,B(-1,2)是一次函数
,B(-1,2)是一次函数 与反比例函数
与反比例函数
 )图象的两个交点,AC⊥x轴于C,BD⊥y轴于D。
)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D。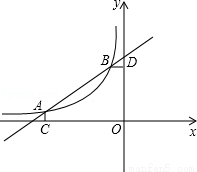
 .
.
 B.
B. C.
C. D.
D.