题目内容
 已知:如图,正方形ABCD的边长为6,E为DC中点,将△ADE沿AE折叠,D点落在D1处,连结AD1并延长交BC于F处,求线段BF的长.
已知:如图,正方形ABCD的边长为6,E为DC中点,将△ADE沿AE折叠,D点落在D1处,连结AD1并延长交BC于F处,求线段BF的长.分析:连接EF,先由折叠的性质得出AD=AD1=6,DE=D1E=3,再利用HL证明△ED1F≌△ECF,得出D1F=CF,设D1F=x,则AF=6+x,BF=6-x,然后在Rt△ABF中,运用勾股定理得出AB2+BF2=AF2,列出方程62+(6-x)2=(6+x)2,解方程求出x的值,进而得到BF的长.
解答: 解:如图,连接EF.
解:如图,连接EF.
由折叠的性质知:AD=AD1=6,DE=D1E=3.
在△ED1F与△ECF中,∠ED1F=∠C=90°,
,
∴△ED1F≌△ECF(HL),
∴D1F=CF.
设D1F=x,则CF=x,AF=6+x,BF=6-x,
在Rt△ABF中,由勾股定理可得:AB2+BF2=AF2,
即62+(6-x)2=(6+x)2,解得x=
,
∴BF=6-
=
.
 解:如图,连接EF.
解:如图,连接EF.由折叠的性质知:AD=AD1=6,DE=D1E=3.
在△ED1F与△ECF中,∠ED1F=∠C=90°,
|
∴△ED1F≌△ECF(HL),
∴D1F=CF.
设D1F=x,则CF=x,AF=6+x,BF=6-x,
在Rt△ABF中,由勾股定理可得:AB2+BF2=AF2,
即62+(6-x)2=(6+x)2,解得x=
| 3 |
| 2 |
∴BF=6-
| 3 |
| 2 |
| 9 |
| 2 |
点评:本题考查了正方形的性质,轴对称的性质,勾股定理,全等三角形的判定与性质,有一定难度.通过作辅助线证明△ED1F≌△ECF,进而得出D1F=CF是解题的关键.

练习册系列答案
相关题目
 ,连接DF,交BE的延长线于点G,连接OG.
,连接DF,交BE的延长线于点G,连接OG.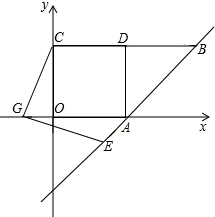
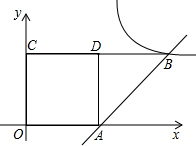
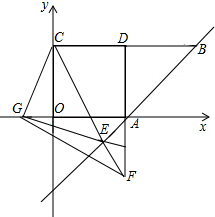



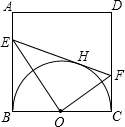 于E,交CD于F.
于E,交CD于F. 已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.
已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.