题目内容
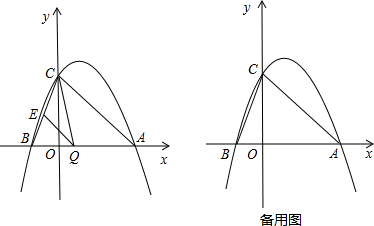
已知抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(O,4),与x轴交于点A、B,点A的坐标为(4,0)(1)求该抛物线解析式;
(2)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接OQ,当△OQE的面积最大时,求Q点坐标;
(3)作平行于x轴的直线MN交抛物线于M、N点,以线段MN的长为直径作圆,当直线MN运动到何处时,以线段MN为直径的圆与X轴相切?写出过程;
(4)线段CA上的动点P自C向A以每秒
| 2 |
分析:(1)根据抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(O,4),与x轴交于点A(4,0),将经过的两点的坐标代入到二次函数中即可求得二次函数的解析式;
(2)设Q(m,0),可求得B(-2,0),|BA|=6,|BQ|=m+2,根据QE∥AC得到△BQE∽△BAC,利用相似三角形面积的比等于相似比的平方表示出三角形BEQ的面积,进而表示出三角形CQE的面积,求出最大值即可;
(3)由对称性和垂径定理知,圆心必在抛物线对称轴上,抛物线对称轴为x=1.然后分当圆心在x轴上方时和当圆心在x轴下方时,两种情况求得r的值即可;
(4)分△APQ∽△ACB和△APQ∽△ABC两种情况求得t的值.
(2)设Q(m,0),可求得B(-2,0),|BA|=6,|BQ|=m+2,根据QE∥AC得到△BQE∽△BAC,利用相似三角形面积的比等于相似比的平方表示出三角形BEQ的面积,进而表示出三角形CQE的面积,求出最大值即可;
(3)由对称性和垂径定理知,圆心必在抛物线对称轴上,抛物线对称轴为x=1.然后分当圆心在x轴上方时和当圆心在x轴下方时,两种情况求得r的值即可;
(4)分△APQ∽△ACB和△APQ∽△ABC两种情况求得t的值.
解答:解:(1)∵抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(O,4),与x轴交于点A、B,点A的坐标为(4,0)
∴
解得:
∴函数关系式为y=-
x2+x+4;
(2)设Q(m,0),
可求得B(-2,0),|BA|=6,|BQ|=m+2,
因QE∥AC,∴△BQE∽△BAC,∴
=
,
∴S△BEQ=
.S△CQE=S△BQC-SBEQ=-
(m-1)2+3(-2<m<4),
当m=1时,面积最大,此时Q(1,0);
(3)由对称性和垂径定理知,圆心必在抛物线对称轴上,
抛物线对称轴为x=1.当圆心在x轴上方时,设圆心坐标为(1,r),(r>0).
则M(1-r,r),将M点的坐标代入抛物线解析式中得:r=-
(1-r)2+1-r+4,
解得r=
-1.当圆心在x轴下方时,可求得r=-
-1,
所以当MN所在的直线解析式为y=
-1或y=-
-1时,
以线段MN为直径的圆与x轴相切;
(4)若△APQ∽△ACB时,t=2.4;
若△APQ∽△ABC时,t=
.
∴
|
解得:
|
∴函数关系式为y=-
| 1 |
| 2 |
(2)设Q(m,0),
可求得B(-2,0),|BA|=6,|BQ|=m+2,
因QE∥AC,∴△BQE∽△BAC,∴
| S△BEQ |
| S△ABC |
| BQ2 |
| BA2 |
∴S△BEQ=
| (m+2)2 |
| 3 |
| 1 |
| 3 |
当m=1时,面积最大,此时Q(1,0);
(3)由对称性和垂径定理知,圆心必在抛物线对称轴上,
抛物线对称轴为x=1.当圆心在x轴上方时,设圆心坐标为(1,r),(r>0).
则M(1-r,r),将M点的坐标代入抛物线解析式中得:r=-
| 1 |
| 2 |
解得r=
| 10 |
| 10 |
所以当MN所在的直线解析式为y=
| 10 |
| 10 |
以线段MN为直径的圆与x轴相切;
(4)若△APQ∽△ACB时,t=2.4;
若△APQ∽△ABC时,t=
| 16 |
| 7 |
点评:本题考查了二次函数的综合知识,这类题目往往出现在中考试题的最后一个题中,难度相对较大.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 与x轴的另一个交点为E.
与x轴的另一个交点为E. 如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=
如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=