题目内容
在△ABC中,点D、E、F顺次在边AB、BC、CA上,设AD=p•AB,BE=q•BC,CF=r•CA,其中p、q、r是正数,且使p+q+r=| 2 |
| 3 |
| 2 |
| 5 |
分析:首先根据三角形面积关系求得S△ADF=(1-r)•p•S△ABC,S△BDE=(1-q)•r•S△ABC,S△EFC=(1-p)•q•S△ABC,又由(p+q+r)2=(p2+q2+r2)+2(pr+qr+pq),p+q+r=
,p2+q2+r2=
,则可求得答案.
| 2 |
| 3 |
| 2 |
| 5 |
解答: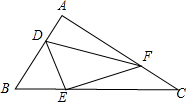 解:如图:
解:如图:
∵AD=p•AB,BE=q•BC,CF=r•CA,
∴S△ADF=(1-r)•p•S△ABC,S△BDE=(1-q)•r•S△ABC,S△EFC=(1-p)•q•S△ABC,
∴S△DEF=S△ABC-S△ADF-S△BDE-S△EFC=[1-(1-r)•p-(1-q)•r-(1-p)•q]•S△ABC=[1-(p+q+r)+(pr+qy+pq)]•S△ABC,
∵(p+q+r)2=(p2+q2+r2)+2(pr+qr+pq),p+q+r=
,p2+q2+r2=
,
∴pr+qr+pq=
[(p+q+r)2-(p2+q2+r2)]=
,
∴S△DEF=(1-
+
)•S△ABC=
S△ABC,
∴S△DEF:S△ABC=16:45.
故答案为:16:45.
 解:如图:
解:如图:∵AD=p•AB,BE=q•BC,CF=r•CA,
∴S△ADF=(1-r)•p•S△ABC,S△BDE=(1-q)•r•S△ABC,S△EFC=(1-p)•q•S△ABC,
∴S△DEF=S△ABC-S△ADF-S△BDE-S△EFC=[1-(1-r)•p-(1-q)•r-(1-p)•q]•S△ABC=[1-(p+q+r)+(pr+qy+pq)]•S△ABC,
∵(p+q+r)2=(p2+q2+r2)+2(pr+qr+pq),p+q+r=
| 2 |
| 3 |
| 2 |
| 5 |
∴pr+qr+pq=
| 1 |
| 2 |
| 1 |
| 45 |
∴S△DEF=(1-
| 2 |
| 3 |
| 1 |
| 45 |
| 16 |
| 45 |
∴S△DEF:S△ABC=16:45.
故答案为:16:45.
点评:此题考查了三角形面积之间的关系以及完全平方公式的变形.此题难度较大,注意数形结合与整体思想的应用.

练习册系列答案
相关题目
 ∠ACB的外角平分线于点F.
∠ACB的外角平分线于点F. 如图,在△ABC中,点D,E分别在边AB,AC上,给出5个论断:①CD⊥AB;②BE⊥AC;③AE=CE;④∠ABE=30°;⑤CD=BE.
如图,在△ABC中,点D,E分别在边AB,AC上,给出5个论断:①CD⊥AB;②BE⊥AC;③AE=CE;④∠ABE=30°;⑤CD=BE.
 (2013•上海)如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么CF:CB等于( )
(2013•上海)如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么CF:CB等于( )