题目内容
等边三角形ABC的边AB在直线l上,动点D也在直线l上(不与A,B点重合),△ADE为等边三角形.
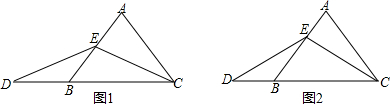
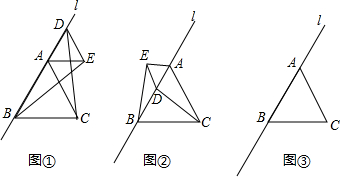
(1)如图①,当点D在线段BA的延长线上且△ADE与△ABC在直线l的同侧时,试猜想线段BE与CD的大小关系为______
(2)如图②,当点D在线段BA上且ADE与ABC在直线l异测时,(1)中的结论是否仍然成立?若不成立,请说明结论发生了怎样的变化;若成立,说明理由,并求出此时线段BE与CD所在直线的夹角α(0°<α<90°)
(3)当点D在线段AB的延长线上且△ADE与△ABC仍然在直线l的异测时,试在图中画③出相应的图形,并直接判断此时BE与CD的关系(不必说明理由).
解:(1)BE=CD
∵△ABC和△ADE都是等边三角形,
∴AB=BC=AC,AD=DE=AE,∠ABC=∠BCA=∠BAC=∠DAE=∠ADE=∠AED=60°.
∴∠BAC+∠EAC=∠DAE+∠CAE,
即∠BAE=∠DAC,
在△BAE和△CAD中,
 ,
,
∴△BAE≌△CAD,
∴BE=CD.
故答案为:BE=CD.
(2)(1)中的结论仍然成立,BE=CD.
∵△ABC和△ADE都是等边三角形,
∴AB=BC=AC,AD=DE=AE,∠ABC=∠BCA=∠BAC=∠DAE=∠ADE=∠AED=60°.
在△BAE和△CAD中,

∴△BAE≌△CAD,
∴BE=CD.∠ACD=∠ABE.
延长CD到F交BE于点F,
∴∠BCD+∠DBE=60°,
∴∠BFC=60°.
∴线段BE与CD所在直线的夹角α为60°.
(3)如图③BE=CD,
∵△ABC和△ADE都是等边三角形,
∴AB=BC=AC,AD=DE=AE,∠ABC=∠BCA=∠BAC=∠DAE=∠ADE=∠AED=60°,
∴∠BAE=∠DAC=120°.
在△BAE和△CAD中,
 ,
,
∴∴△BAE≌△CAD,
∴BE=CD.
分析:(1)如图①根据等边三角形的性质证明△BAE≌△CAD,就可以得出BE=CD;
(2)如图②根据等边三角形的性质证明△BAE≌△CAD,就可以得出BE=CD;
(3)如图③根据等边三角形的性质证明△BAE≌△CAD,就可以得出BE=CD;
点评:本题考查了等边三角形的性质及全能等三角形的判定及性质的运用,在解答过程中合理利用等边三角形的边角的性质是解答本题的关键.
∵△ABC和△ADE都是等边三角形,
∴AB=BC=AC,AD=DE=AE,∠ABC=∠BCA=∠BAC=∠DAE=∠ADE=∠AED=60°.
∴∠BAC+∠EAC=∠DAE+∠CAE,
即∠BAE=∠DAC,
在△BAE和△CAD中,
 ,
,∴△BAE≌△CAD,
∴BE=CD.
故答案为:BE=CD.

(2)(1)中的结论仍然成立,BE=CD.
∵△ABC和△ADE都是等边三角形,
∴AB=BC=AC,AD=DE=AE,∠ABC=∠BCA=∠BAC=∠DAE=∠ADE=∠AED=60°.
在△BAE和△CAD中,

∴△BAE≌△CAD,
∴BE=CD.∠ACD=∠ABE.
延长CD到F交BE于点F,
∴∠BCD+∠DBE=60°,
∴∠BFC=60°.
∴线段BE与CD所在直线的夹角α为60°.
(3)如图③BE=CD,
∵△ABC和△ADE都是等边三角形,
∴AB=BC=AC,AD=DE=AE,∠ABC=∠BCA=∠BAC=∠DAE=∠ADE=∠AED=60°,
∴∠BAE=∠DAC=120°.
在△BAE和△CAD中,
 ,
,∴∴△BAE≌△CAD,
∴BE=CD.
分析:(1)如图①根据等边三角形的性质证明△BAE≌△CAD,就可以得出BE=CD;
(2)如图②根据等边三角形的性质证明△BAE≌△CAD,就可以得出BE=CD;
(3)如图③根据等边三角形的性质证明△BAE≌△CAD,就可以得出BE=CD;
点评:本题考查了等边三角形的性质及全能等三角形的判定及性质的运用,在解答过程中合理利用等边三角形的边角的性质是解答本题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
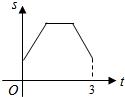
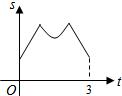
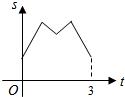
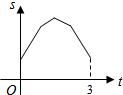
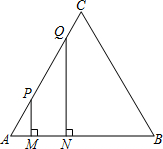 线段MN运动的时间为t秒.
线段MN运动的时间为t秒.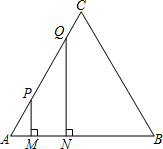 如图,等边三角形ABC的边长为4厘米,长为1厘米的线段MN在△ABC的边AB上沿AB方向以1厘米/秒的速度向B点运动(运动开始时,点M与点A重合,点N到达点B时运动终止),过点M、N分别作AB边的垂线,与△ABC的其它边交于P、Q两点.线段MN在运动的过程中,四边形MNQP的面积为S,运动的时间为t.则大致反映S与t变化关系的图象是( )
如图,等边三角形ABC的边长为4厘米,长为1厘米的线段MN在△ABC的边AB上沿AB方向以1厘米/秒的速度向B点运动(运动开始时,点M与点A重合,点N到达点B时运动终止),过点M、N分别作AB边的垂线,与△ABC的其它边交于P、Q两点.线段MN在运动的过程中,四边形MNQP的面积为S,运动的时间为t.则大致反映S与t变化关系的图象是( )