题目内容

（2013•梧州一模）如图，用火柴棒摆出一系列等边三角形图案，按这种方式摆下去，摆出第n个图案需要用
3n(n+1)
2
3n(n+1)
2
根火柴棒（用含n的代数式表示）．
分析：结合图形计算前三个图形中的火柴数时，即可发现规律．
解答：解：当n=1时，需要火柴3×1=3，当n=2时，需要火柴3×（1+2）=9；当n=3时，需要火柴3×（1+2+3）=18，…，
依此类推，第n个图形共需火柴3×（1+2+3+…+n）=
3n(n+1)
2
，
故答案为：
3n(n+1)
2
．
点评：本题主要考查了根据题意找出规律：1+2+3+…+n=
3n(n+1)
2
，难度适中．
练习册系列答案
相关题目
（2013•梧州一模）用科学记数法表示2175000000为（　　）
（2013•梧州一模）一组数据2、0、3、2、3、1、x的众数是3，则这组数据从小到大排列的中位数是
2
2
．
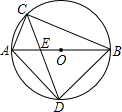（2013•梧州一模）已知在⊙O中，直径AB为10cm，弦AC为6cm，∠ACB的平分线交⊙O于D，交AB于E，则CD的长是
7
2
7
2
．
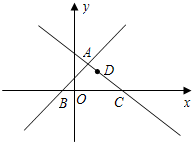（2013•梧州一模）如图，在平面直角坐标系xOy中，直线y=x+1与y=-
3
4
x+3交于点A，分别交x轴于点B和点C，点D是直线AC上且位于y轴右侧的一个动点．
（1）点A，B，C的坐标是A
（
8
7
，
15
7
）
（
8
7
，
15
7
）
，B
（-1，0）
（-1，0）
，C
（4，0）
（4，0）
．
（2）当△CBD为等腰三角形时，点D的坐标是
（
3
2
，
15
8
）或（8，-3）
（
3
2
，
15
8
）或（8，-3）
．
（3）在（2）中，当点D在第四象限时，过点D的反比例函数解析式是
y=-
24
x
y=-
24
x
．
（2013•梧州一模）如图，在3×3的正方形网格中，每个小正方形的边长为1，A、B两点在网格格点上，若C点也在网格格点上，以A、B、C三点为顶点的三角形的面积为1，则满足条件的点C的个数是（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网