Question

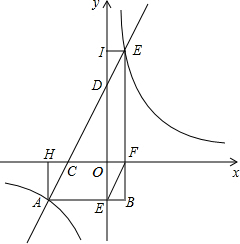（2013•苏州一模）如图，一直线与反比例函数y=

k

x

（k＞0）交于A、B两点，直线与x轴，y轴分别交于C，D两点，过A，B两点分别向x轴，y轴作垂线，H、E、F、I为垂足，BF与AE交于G点．
（1）矩形OFBI与矩形OHAE的面积和为

2k

；（用含七的代数式表示）；
（2）求证：①AG•GF=EG•GB；②AC=BD；
（3）若直线AB的解析式为y=2x+2，且AB=2CD，反比例函数解析式为

y=

3

2x

．

Answer 1

分析：（1）根据反比例函数y=

k

x

的几何意义得到S_矩形OFBI=k，S_矩形OHAE=k，则矩形OFBI与矩形OHAE的面积和为2k；
（2）根据（1）的结论易得S_矩形AGFH=S_矩形BIEG，根据矩形的面积公式得到AG•GF=EG•GB；由AG•GF=EG•GB变形得GE：GA=GF：GB，而∠EGF=∠AGB，根据相似的判定方法得到△EGF∽△AGB，则∠GAB=∠GEF，所以EF∥AB，根据平行四边形的判定方法得到四边形AEFC、四边形BDEF都是平行四边形，于是AC=EF，EF=BD，即可得到AC=BD；
（3）先确定C点坐标（-1，0），D点坐标（0，2），再计算出CD=

5

，利用AB=2CD，AC=BD得到BD=

5

2

，设B点坐标为（a，a+2），在Rt△BDI中利用勾股定理得到a²+（2a）²=（

1

2

5

）²，解得a₁=

1

2

，a₂=-

1

2

（舍去），则B点坐标为（

1

2

，3），然后利用待定系数法即可确定反比例函数解析式．

解答：（1）解：∵S_矩形OFBI=k，S_矩形OHAE=k，
∴矩形OFBI与矩形OHAE的面积和为2k；

（2）证明：①∵S_矩形OFBI=S_矩形OHAE，
∴S_矩形OFBI+S_矩形OEGF=S_矩形OHAE+S_矩形OEGF，
∴S_矩形AGFH=S_矩形BIEG，
∴AG•GF=EG•GB；
②∵AG•GF=EG•GB，
∴GE：GA=GF：GB，
∵∠EGF=∠AGB，
∴△EGF∽△AGB，
∴∠GAB=∠GEF，
∴EF∥AB，
∵CF∥AE，BF∥DE，
∴四边形AEFC、四边形BDEF都是平行四边形，
∴AC=EF，EF=BD，
∴AC=BD；

（3）∵直线AB的解析式为y=2x+2，
∴C点坐标为（-1，0），D点坐标为（0，2），
∴CD=

OC2+OD2

=

5

，
∵AB=2CD，AC=BD，
∴BD=

5

2

，
设B点坐标为（a，a+2），
在Rt△BDI中，BI=a，ID=2a+2-2=2a，
∴a²+（2a）²=（

1

2

5

）²，解得a₁=

1

2

，a₂=-

1

2

（舍去），
∴B点坐标为（

1

2

，3），
把B（

1

2

，3）代入y=

k

x

得k=

1

2

×3=

3

2

，
∴反比例函数解析式为y=

3

2x

．
故答案为：2k；y=

3

2x

．

点评：本题考查了反比例函数的综合题：掌握反比例函数图象上点的坐标特征、比例系数的几何意义和矩形和平时四边形的判定与性质；熟练运用勾股定理和相似比进行几何计算．