题目内容
一元二次方程:(m-1)x2+(m2-3m+2)x-8=0互为相反数根,则m=( )
分析:根据一元二次方程的定义得m-1≠0,再根据根与系数的关系得到-
=0,解得m=1或2,然后舍去m=1,于是得到m=2.
| m2-3m+2 |
| m-1 |
解答:解:设方程的两根为x1,x2,
根据题意得m-1≠0且x1+x2=-
=0,
∴m=2.
故选B.
根据题意得m-1≠0且x1+x2=-
| m2-3m+2 |
| m-1 |
∴m=2.
故选B.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程的两根为x1,x2,则x1+x2=-
,x1•x2=
.也考查了一元二次方程的定义.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
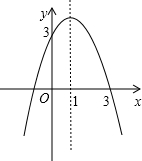 已知二次函数y=-x2+bx+c的图象如图所示,解决下列问题:
已知二次函数y=-x2+bx+c的图象如图所示,解决下列问题: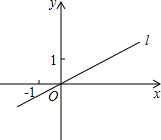 如图,在平面直角坐标系中,直线l的解析式为y=
如图,在平面直角坐标系中,直线l的解析式为y=