题目内容
 如图,△ABC是等边三角形,P是BC上任意一点,PD⊥AB,PE⊥AC,连接DE.记△ADE的周长为L1,四边形BDEC的周长为L2,则L1与L2的大小关系是
如图,△ABC是等边三角形,P是BC上任意一点,PD⊥AB,PE⊥AC,连接DE.记△ADE的周长为L1,四边形BDEC的周长为L2,则L1与L2的大小关系是
- A.Ll=L2
- B.L1>L2
- C.L2>L1
- D.无法确定
A
分析:等边三角形各内角为60°,故∠B=∠C=60°,即可求得BP=2BD,CP=2CE,∴BD+CE= BC,即可求得L1=L2.
BC,即可求得L1=L2.
解答:∵等边三角形各内角为60°,∴∠B=∠C=60°,
∵∠BPD=∠CPE=30°,
∴在Rt△BDP和Rt△CEP中,
∴BP=2BD,CP=2CE,
∴BD+CE= BC,
BC,
∴AD+AE=AB+AC- BC=
BC= BC,
BC,
∴BD+CE+BC= BC,
BC,
L1= BC+DE,
BC+DE,
L2= BC+DE,
BC+DE,
即得L1=L2,
故选 A.
点评:本题考查了直角三角形中特殊角的正弦函数值,考查了等边三角形各边相等的性质,本题中求证L1= BC+DE,L2=
BC+DE,L2= BC+DE是解题的关键.
BC+DE是解题的关键.
分析:等边三角形各内角为60°,故∠B=∠C=60°,即可求得BP=2BD,CP=2CE,∴BD+CE=
 BC,即可求得L1=L2.
BC,即可求得L1=L2.解答:∵等边三角形各内角为60°,∴∠B=∠C=60°,
∵∠BPD=∠CPE=30°,
∴在Rt△BDP和Rt△CEP中,
∴BP=2BD,CP=2CE,
∴BD+CE=
 BC,
BC,∴AD+AE=AB+AC-
 BC=
BC= BC,
BC,∴BD+CE+BC=
 BC,
BC,L1=
 BC+DE,
BC+DE,L2=
 BC+DE,
BC+DE,即得L1=L2,
故选 A.
点评:本题考查了直角三角形中特殊角的正弦函数值,考查了等边三角形各边相等的性质,本题中求证L1=
 BC+DE,L2=
BC+DE,L2= BC+DE是解题的关键.
BC+DE是解题的关键. 
练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
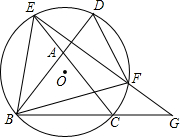 ∥AC,EF的延长线交BC的延长线于点G.
∥AC,EF的延长线交BC的延长线于点G. 9、如图,△ABC是等边三角形,过AB边上一点D作BC的平行线交AC于E,则△ADE的三个内角
9、如图,△ABC是等边三角形,过AB边上一点D作BC的平行线交AC于E,则△ADE的三个内角 如图,△ABC是等边三角形,AB=4cm,则BC边上的高AD等于
如图,△ABC是等边三角形,AB=4cm,则BC边上的高AD等于 如图,△ABC是等边三角形,D为BC边上的点,∠BAD=15°,将△ABD绕点A点逆时针方向旋转后到达△ACE的位置,那么旋转角的度数是
如图,△ABC是等边三角形,D为BC边上的点,∠BAD=15°,将△ABD绕点A点逆时针方向旋转后到达△ACE的位置,那么旋转角的度数是 如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.
如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.