题目内容
 如图AB是⊙O的直径,C是半圆上的一个三等分点,D是
如图AB是⊙O的直径,C是半圆上的一个三等分点,D是 的中点,P是直径AB上的一动点,⊙O的半径为1,则PC+PD的最小值为
的中点,P是直径AB上的一动点,⊙O的半径为1,则PC+PD的最小值为
- A.1
- B.

- C.

- D.

B
分析:作D关于AB的对称点E,则根据垂径定理得:E在⊙O上,连接EC交AB于P′,作直径EF,连接DP′,CP′CF,
则若P在P′时,DP+CP最小,根据解直角三角形求出CE,根据轴对称求出DP′+CP′=CE即可.
解答: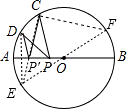
作D关于AB的对称点E,则根据垂径定理得:E在⊙O上,连接EC交AB于P′,作直径EF,连接DP′,CP′CF,
则若P在P′时,DP+CP最小,
∵C是半圆上的一个三等分点,D是 的中点,
的中点,
∴∠F= ×(60°+30°)=45°,
×(60°+30°)=45°,
∵EF为直径,
∴∠ECF=90°,EF=2,
即sin45°= ,
,
∴CE= ,
,
∵D关于AB的对称点E,
∴DP′=EP′,
∴DP+CP=CE,
即DP+CP= ,
,
故选B.
点评:本题考查了解直角三角形,圆周角定理,垂径定理,轴对称的性质等知识点的应用,主要考查学生的推理和计算能力.
分析:作D关于AB的对称点E,则根据垂径定理得:E在⊙O上,连接EC交AB于P′,作直径EF,连接DP′,CP′CF,
则若P在P′时,DP+CP最小,根据解直角三角形求出CE,根据轴对称求出DP′+CP′=CE即可.
解答:

作D关于AB的对称点E,则根据垂径定理得:E在⊙O上,连接EC交AB于P′,作直径EF,连接DP′,CP′CF,
则若P在P′时,DP+CP最小,
∵C是半圆上的一个三等分点,D是
 的中点,
的中点,∴∠F=
 ×(60°+30°)=45°,
×(60°+30°)=45°,∵EF为直径,
∴∠ECF=90°,EF=2,
即sin45°=
 ,
,∴CE=
 ,
,∵D关于AB的对称点E,
∴DP′=EP′,
∴DP+CP=CE,
即DP+CP=
 ,
,故选B.
点评:本题考查了解直角三角形,圆周角定理,垂径定理,轴对称的性质等知识点的应用,主要考查学生的推理和计算能力.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
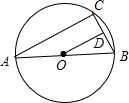 如图AB是⊙O的直径,C是⊙O上的一点,若AC=8cm,AB=10cm,OD⊥BC于点D,求BD的长.
如图AB是⊙O的直径,C是⊙O上的一点,若AC=8cm,AB=10cm,OD⊥BC于点D,求BD的长.
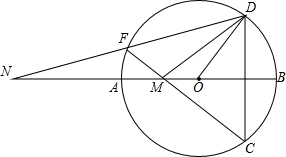 CF交AB于点M,连接DF并延长交BA的延长线于点N.
CF交AB于点M,连接DF并延长交BA的延长线于点N. 如图AB是⊙O的直径,∠D=35°,则∠AOC=
如图AB是⊙O的直径,∠D=35°,则∠AOC= (2012•自贡)如图AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.
(2012•自贡)如图AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C. (2013•南昌)如图AB是半圆的直径,图1中,点C在半圆外;图2中,点C在半圆内,请仅用无刻度的直尺按要求画图.
(2013•南昌)如图AB是半圆的直径,图1中,点C在半圆外;图2中,点C在半圆内,请仅用无刻度的直尺按要求画图.