题目内容
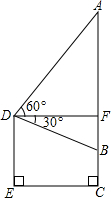（2012•宿迁）如图是使用测角仪测量一幅壁画高度的示意图，已知壁画AB的底端距离地面的高度BC=1m，在壁画的正前方点D处测得壁画底端的俯角∠BDF=30°，且点D距离地面的高度DE=2m，求壁画AB的高度．分析：先过点B作BG⊥DE于点G，由于DE⊥CE，EC⊥CE，DF⊥AC，故四边形DECF是矩形，BC=1m，DE=2m，所以EG=BC=1m，故DG=BF=1m，在Rt△DBF中，由锐角三角函数的定义可求出DF的长，同理在Rt△ADF中由锐角三角函数的定义可求出AF的长，根据AB=AF+BF即可得出结论．
解答：
解：先过点B作BG⊥DE于点G．
∵DE⊥CE，EC⊥CF，DF⊥AC，
∴四边形DECF是矩形，
∵BC=1m，DE=2m，
∴EG=BC=1m，DG=BF=1m，
在Rt△DBF中，
∵∠BDF=30°，BF=1m，
∴DF=
=
=
，
同理，在Rt△ADF中，
∵∠ADF=60°，DF=
，
∴AF=DF•tan60°=
×
=3m．
∴AB=AF+BF=3+1=4m．
答：壁画AB的高度是4米．
解：先过点B作BG⊥DE于点G．∵DE⊥CE，EC⊥CF，DF⊥AC，
∴四边形DECF是矩形，
∵BC=1m，DE=2m，
∴EG=BC=1m，DG=BF=1m，
在Rt△DBF中，
∵∠BDF=30°，BF=1m，
∴DF=
| BF |
| tan30° |
| 1 | ||||
|
| 3 |
同理，在Rt△ADF中，
∵∠ADF=60°，DF=
| 3 |
∴AF=DF•tan60°=
| 3 |
| 3 |
∴AB=AF+BF=3+1=4m．
答：壁画AB的高度是4米．
点评：本题考查的是解直角三角形的应用-仰角俯角问题，熟知锐角三角函数的定义是解答此题的关键．
练习册系列答案
相关题目
（2012•宿迁）如图，SO，SA分别是圆锥的高和母线，若SA=12cm，∠ASO=30°，则这个圆锥的侧面积是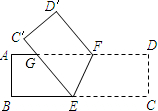
（2012•宿迁）如图，将一张矩形纸片ABCD沿EF折叠，使顶点C，D分别落在点C′，D′处，C′E交AF于点G，若∠CEF=70°，则∠GFD′=
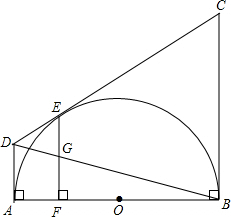（2012•宿迁）如图，在四边形ABCD中，∠DAB=∠ABC=90°，CD与以AB为直径的半圆相切于点E，EF⊥AB于点F，EF交BD于点G，设AD=a，BC=b．
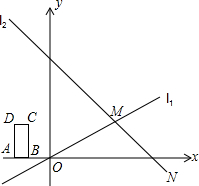直线l2与x轴相交于点N．