题目内容
17.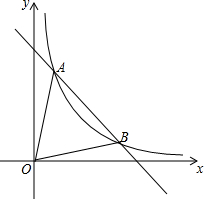 如图,一次函数y=-x+6的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B两点.
如图,一次函数y=-x+6的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于A(1,n)和B两点.(1)求反比例函数的解析式;
(2)求△AOB的面积.
分析 (1)把A(1,n)代入y=-x+6即可求得n=5,然后把(1,5)代入y=$\frac{k}{x}$,根据待定系数法即可求得解析式;
(2)根据△AOB的面积等于大的三角形减去两个小的三角形的面积求得即可.
解答 解:(1)∵点A(1,n)在一次函数y=-x+6的图象上,
∴n=-1+6=5,
∴A(1,5),
∵点A(1,n)在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,
∴k=1×5=5,
∴反比例函数的解析式为y=$\frac{5}{x}$;
(2)由$\left\{\begin{array}{l}{y=-x+6}\\{y=\frac{5}{x}}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=1}\\{y=5}\end{array}\right.$或$\left\{\begin{array}{l}{x=5}\\{y=1}\end{array}\right.$,
∴A(1,5),B(5,1),
由直线y=-x+6可知,直线与坐标轴的交点为(6,0),(0,6),
∴S△AOB=$\frac{1}{2}$×6×6-$\frac{1}{2}$×6×1-$\frac{1}{2}$×6×1=12.
点评 此题考查了反比例函数与一次函数交点问题、待定系数法求函数的解析式以及三角形面积问题.注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
9.下面的说法中,正确的是( )
| A. | -3和-1之间的有理数是-2 | |
| B. | 数轴上表示-a的点一定在原点的左边 | |
| C. | 在数轴上离开原点的距离越近的点表示的数越小 | |
| D. | -1和-2之间有无数个负数 |


 如图,在菱形ABCD中,∠A=60°,BD=5,则菱形ABCD的周长为20.
如图,在菱形ABCD中,∠A=60°,BD=5,则菱形ABCD的周长为20.