��Ŀ����
 ��ͼ��ֱ��l1��y=x+1��ֱ��l2��
��ͼ��ֱ��l1��y=x+1��ֱ��l2�� �ཻ�ڵ�P��-1��0����ֱ��l1��y�ύ�ڵ�A��һ����C�ӵ�A����������ƽ����x��ķ����˶�������ֱ��l2�ϵĵ�B1����Ϊ��ֱ��x��ķ����˶�������ֱ��l1�ϵĵ�A1��������ƽ����x��ķ����˶�������ֱ��l2�ϵĵ�B2�����ָ�Ϊ��ֱ��x��ķ����˶�������ֱ��l1�ϵĵ�A2��������ƽ����x��ķ����˶������մ˹����˶�������C���ξ�����B1��A1��B2��A2��B3��A3������Bn��An����
�ཻ�ڵ�P��-1��0����ֱ��l1��y�ύ�ڵ�A��һ����C�ӵ�A����������ƽ����x��ķ����˶�������ֱ��l2�ϵĵ�B1����Ϊ��ֱ��x��ķ����˶�������ֱ��l1�ϵĵ�A1��������ƽ����x��ķ����˶�������ֱ��l2�ϵĵ�B2�����ָ�Ϊ��ֱ��x��ķ����˶�������ֱ��l1�ϵĵ�A2��������ƽ����x��ķ����˶������մ˹����˶�������C���ξ�����B1��A1��B2��A2��B3��A3������Bn��An����
����C����An��ʱ���˶�����·���ij�Ϊ
- A.n2
- B.2n-1
- C.2n-1+1
- D.2n+1-2
D
��������ֱ��ֱ��l1��y=x+1��֪��A��0��1������B1������Ϊ1������ֱ��l2��y= x+
x+ �У���B1��1��1������A1��B1��������ȣ��ɵ�A1��1��2������AB1=1��A1B1=2-1=1�����жϡ�AA1B1Ϊ����ֱ�������Σ�����ƽ���ߵ����ʣ��á�A1A2B2����A2A3B3���������ǵ���ֱ�������Σ�����ƽ����x���ֱ����������������ȣ�ƽ����y���ֱ���������������ȣ���ֱ��l1��l2�Ľ���ʽ���ֱ���AB1+A1B1��A1B2+A2B2�ij����ó�һ����ɣ�
�У���B1��1��1������A1��B1��������ȣ��ɵ�A1��1��2������AB1=1��A1B1=2-1=1�����жϡ�AA1B1Ϊ����ֱ�������Σ�����ƽ���ߵ����ʣ��á�A1A2B2����A2A3B3���������ǵ���ֱ�������Σ�����ƽ����x���ֱ����������������ȣ�ƽ����y���ֱ���������������ȣ���ֱ��l1��l2�Ľ���ʽ���ֱ���AB1+A1B1��A1B2+A2B2�ij����ó�һ����ɣ�
�����ֱ��ֱ��l1��y=x+1��֪��A��0��1��������ƽ����x���ֱ����������������ȣ�ƽ����y���ֱ���������������ȣ���ֱ��l1��l2�Ľ���ʽ��֪��B1��1��1����AB1=1��
A1��1��2����A1B1=2-1=1��AB1+A1B1=2��
B2��3��2����A2��3��4����A1B2=3-1=2��A2B2=4-2=2��A1B2+A2B2=2+2=4=22��
����
�ɴ˿ɵ�An-1Bn+AnBn=2n��
���ԣ�������C����An��ʱ���˶�����·���ij�Ϊ2+22+23+..+2n=2n+1-2��
��ѡD��
���������⿼����һ�κ������ۺ����ã��ؼ�������ƽ����x���ֱ���ϵ����������ȣ�ƽ����y���ֱ���ϵ�ĺ�������ȣ��ó�������꣬�жϵ���ֱ�������Σ��ó�һ����ɣ�
��������ֱ��ֱ��l1��y=x+1��֪��A��0��1������B1������Ϊ1������ֱ��l2��y=
 x+
x+ �У���B1��1��1������A1��B1��������ȣ��ɵ�A1��1��2������AB1=1��A1B1=2-1=1�����жϡ�AA1B1Ϊ����ֱ�������Σ�����ƽ���ߵ����ʣ��á�A1A2B2����A2A3B3���������ǵ���ֱ�������Σ�����ƽ����x���ֱ����������������ȣ�ƽ����y���ֱ���������������ȣ���ֱ��l1��l2�Ľ���ʽ���ֱ���AB1+A1B1��A1B2+A2B2�ij����ó�һ����ɣ�
�У���B1��1��1������A1��B1��������ȣ��ɵ�A1��1��2������AB1=1��A1B1=2-1=1�����жϡ�AA1B1Ϊ����ֱ�������Σ�����ƽ���ߵ����ʣ��á�A1A2B2����A2A3B3���������ǵ���ֱ�������Σ�����ƽ����x���ֱ����������������ȣ�ƽ����y���ֱ���������������ȣ���ֱ��l1��l2�Ľ���ʽ���ֱ���AB1+A1B1��A1B2+A2B2�ij����ó�һ����ɣ������ֱ��ֱ��l1��y=x+1��֪��A��0��1��������ƽ����x���ֱ����������������ȣ�ƽ����y���ֱ���������������ȣ���ֱ��l1��l2�Ľ���ʽ��֪��B1��1��1����AB1=1��
A1��1��2����A1B1=2-1=1��AB1+A1B1=2��
B2��3��2����A2��3��4����A1B2=3-1=2��A2B2=4-2=2��A1B2+A2B2=2+2=4=22��
����
�ɴ˿ɵ�An-1Bn+AnBn=2n��
���ԣ�������C����An��ʱ���˶�����·���ij�Ϊ2+22+23+..+2n=2n+1-2��
��ѡD��
���������⿼����һ�κ������ۺ����ã��ؼ�������ƽ����x���ֱ���ϵ����������ȣ�ƽ����y���ֱ���ϵ�ĺ�������ȣ��ó�������꣬�жϵ���ֱ�������Σ��ó�һ����ɣ�

��ϰ��ϵ�д�
 �żӾ���ϵ�д�
�żӾ���ϵ�д�
�����Ŀ
 20����ͼ��ֱ��l1��y=x+1��ֱ��l2��y=mx+n�ཻ�ڵ�P��a��3���������x�IJ���ʽx+1��mx+n�Ľ⼯Ϊ
20����ͼ��ֱ��l1��y=x+1��ֱ��l2��y=mx+n�ཻ�ڵ�P��a��3���������x�IJ���ʽx+1��mx+n�Ľ⼯Ϊ ��ͼ��ֱ��l1��l2���ڵ�A�������A�����꣮
��ͼ��ֱ��l1��l2���ڵ�A�������A�����꣮ ��ͼ��ֱ��l1��y=2x+4��l2��y=-x-5��ͬһƽ�������ϵ���ཻ�ڵ�P�����P��������
��ͼ��ֱ��l1��y=2x+4��l2��y=-x-5��ͬһƽ�������ϵ���ཻ�ڵ�P�����P��������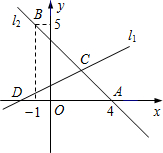 l2���ڵ�C��
l2���ڵ�C�� ��ͼ��ֱ��l1��l2���ڵ�A��ֱ��l2��x�ύ�ڵ�B����y�ύ�ڵ�D��ֱ��l1����Ӧ�ĺ�����ϵʽΪy=-2x+2��
��ͼ��ֱ��l1��l2���ڵ�A��ֱ��l2��x�ύ�ڵ�B����y�ύ�ڵ�D��ֱ��l1����Ӧ�ĺ�����ϵʽΪy=-2x+2��