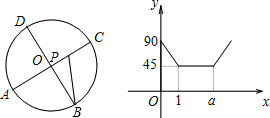
题目内容
如图,A、B、C、D为圆O的四等分点,动点P从圆心O出发,沿扇形DOC的边界:以O→C→D→O路线作匀速运动,设运动时间为
x(s),∠APB=y(°),上图函数图象表示y与x之间函数关系,则a=________.
 π+1
π+1分析:通过函数图象可以得到函数随自变量的变化规律,通过规律结合图象可以求出关键点C、D的坐标值,从而求出横坐标a的值.
解答:根据题意,可知点P从圆心O出发,运动到点C时,∠APB的度数由90°减小到45°,
∴在C点时所对的横坐标为1,
∴OC=1,由弧长公式可以求出弧CD的长度为
 π.
π.当横坐标为a是点P是∠APB由稳定在45°保持不变到增大的转折点;
∴横坐标为a值所对应的点是D点,表示这时P点运动到了D点.
∴a=OC+弧CD的长=
 π+1.
π+1.故答案为:a=
 π+1.
π+1.点评:本题是一道动点问题的函数图象试题,考查了函数图象横、纵坐标表示的意义,让学生对分段函数有一个认识和理解的过程.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB=
14、如图,已知⊙P的半径OD=5,OD⊥AB,垂足是G,OG=3,则弦AB= 如图,已知A,B两点是反比例函数y=
如图,已知A,B两点是反比例函数y=

 如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.
如图AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC于点E.