题目内容
 已知,如图△ABC中,∠ACB的平分线交AB于E,∠ACB的补角∠ACD的平分线为CG,EG∥BC交AC于F,EF会与FG相等吗?为什么?
已知,如图△ABC中,∠ACB的平分线交AB于E,∠ACB的补角∠ACD的平分线为CG,EG∥BC交AC于F,EF会与FG相等吗?为什么?
解:EF=FG,
理由是:∵CE平分∠ACB,CG平分∠ACD,
∴∠BCE=∠ECF,∠DCG=∠GCF,
∵EG∥BC,
∴∠FEC=∠BCE,∠G=∠DCG,
∴∠FEC=∠ECF,∠G=∠FCG,
∴EF=CF,CF=FG,
∴EF=FG.
分析:根据角平分线性质得出∠BCE=∠ECF,∠DCG=∠GCF,根据平行线性质得出∠FEC=∠BCE,∠G=∠DCG,推出∠FEC=∠ECF,∠G=∠FCG,根据等角对等边得出EF=CF,CF=FG,即可推出答案.
点评:本题考查了等腰三角形的性质和判定,平行线性质,角平分线性质等知识点,关键是求出EF=CF,CF=FG,题目具有一定的代表性,是一道比较好的题目.
理由是:∵CE平分∠ACB,CG平分∠ACD,
∴∠BCE=∠ECF,∠DCG=∠GCF,
∵EG∥BC,
∴∠FEC=∠BCE,∠G=∠DCG,
∴∠FEC=∠ECF,∠G=∠FCG,
∴EF=CF,CF=FG,
∴EF=FG.
分析:根据角平分线性质得出∠BCE=∠ECF,∠DCG=∠GCF,根据平行线性质得出∠FEC=∠BCE,∠G=∠DCG,推出∠FEC=∠ECF,∠G=∠FCG,根据等角对等边得出EF=CF,CF=FG,即可推出答案.
点评:本题考查了等腰三角形的性质和判定,平行线性质,角平分线性质等知识点,关键是求出EF=CF,CF=FG,题目具有一定的代表性,是一道比较好的题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
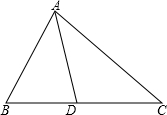 已知,如图△ABC中,AD为△ABC的角平分线,求证:AB•DC=AC•BD.
已知,如图△ABC中,AD为△ABC的角平分线,求证:AB•DC=AC•BD. (1998•河北)已知:如图△ABC中,∠A的平分线AD交BC于D,⊙O过点A,且与BC相切于D,与AB、AC分别相交于E、F,AD与EF相交于G.
(1998•河北)已知:如图△ABC中,∠A的平分线AD交BC于D,⊙O过点A,且与BC相切于D,与AB、AC分别相交于E、F,AD与EF相交于G. 已知:如图△ABC中,∠ACB=90°,D是AC上任意一点,DE⊥AB于E,M,N分别是BD,CE的中点,求证:MN⊥CE.
已知:如图△ABC中,∠ACB=90°,D是AC上任意一点,DE⊥AB于E,M,N分别是BD,CE的中点,求证:MN⊥CE. 已知,如图△ABC中,AB=AC,CD⊥AD于D,CD=
已知,如图△ABC中,AB=AC,CD⊥AD于D,CD= 已知,如图△ABC中,D、E、F分别是三角形三边中点,△ABC的周长为30,面积为48,则△DEF的周长为
已知,如图△ABC中,D、E、F分别是三角形三边中点,△ABC的周长为30,面积为48,则△DEF的周长为