题目内容
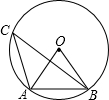 如图,点A、B、C是⊙O上的三点,且△AOB是正三角形,则∠ACB的度数是________.
如图,点A、B、C是⊙O上的三点,且△AOB是正三角形,则∠ACB的度数是________.
30°
分析:先根据等边三角形的性质求出∠AOB的度数,再由圆周角定理即可得出结论.
解答:∵△AOB是正三角形,
∴∠AOB=60°,
∵∠AOB与∠ACB是同弧所对的圆心角与圆周角,
∴∠ACB= ∠AOB=
∠AOB= ×60°=30°.
×60°=30°.
故答案为:30°.
点评:本题考查的是圆周角定理,即在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
分析:先根据等边三角形的性质求出∠AOB的度数,再由圆周角定理即可得出结论.
解答:∵△AOB是正三角形,
∴∠AOB=60°,
∵∠AOB与∠ACB是同弧所对的圆心角与圆周角,
∴∠ACB=
 ∠AOB=
∠AOB= ×60°=30°.
×60°=30°.故答案为:30°.
点评:本题考查的是圆周角定理,即在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 8、如图,点A,B,C是⊙O上的三点,∠BAC=40°,则∠OBC的度数是( )
8、如图,点A,B,C是⊙O上的三点,∠BAC=40°,则∠OBC的度数是( ) 如图,点A、B、C是⊙O上的三点,若∠BOC=50°,则∠A的度数为
如图,点A、B、C是⊙O上的三点,若∠BOC=50°,则∠A的度数为
 如图,点A、B、C是⊙O上的三点,∠BAC=40°,则∠BOC的度数是( )
如图,点A、B、C是⊙O上的三点,∠BAC=40°,则∠BOC的度数是( ) 如图,点A、B、C是圆O上的三点,OB⊥AC,∠BAC=40°,则∠OCA=( )
如图,点A、B、C是圆O上的三点,OB⊥AC,∠BAC=40°,则∠OCA=( )