题目内容
化简:
(1)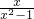 •(
•( -2);
-2);
(2)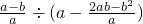 .
.
解:(1)原式= •(
•( )=
)= •
• =-
=- ;
;
(2)原式= ÷(
÷( )=
)= ÷
÷ =
= •
• =
= .
.
分析:(1)先将原式的第一项的分母分解因式,同时将括号里面的两项进行通分,并根据同分母分数的减法法则进行计算,约分后即可得到最简结果;
(2)先对括号里面的两项进行通分,并根据同分母分数的减法法则进行计算,然后根据除以一个数等于乘以这个数的倒数把除法运算化为乘法运算,约分后即可得到最简结果.
点评:此题考查了分式的混合运算,分式的加减运算关键是通分,通分的关键是找最简公分母;分式的乘除运算关键是约分,约分的关键是找公因式,约分时,分式的分子分母出现多项式,应将多项式分解因式后再约分.
 •(
•( )=
)= •
• =-
=- ;
;(2)原式=
 ÷(
÷( )=
)= ÷
÷ =
= •
• =
= .
.分析:(1)先将原式的第一项的分母分解因式,同时将括号里面的两项进行通分,并根据同分母分数的减法法则进行计算,约分后即可得到最简结果;
(2)先对括号里面的两项进行通分,并根据同分母分数的减法法则进行计算,然后根据除以一个数等于乘以这个数的倒数把除法运算化为乘法运算,约分后即可得到最简结果.
点评:此题考查了分式的混合运算,分式的加减运算关键是通分,通分的关键是找最简公分母;分式的乘除运算关键是约分,约分的关键是找公因式,约分时,分式的分子分母出现多项式,应将多项式分解因式后再约分.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
