题目内容
 如图,函数y=ax2-bx+c的图象过点(-1,0),则
如图,函数y=ax2-bx+c的图象过点(-1,0),则| a |
| b+c |
| b |
| c+a |
| c |
| a+b |
-3
-3
.分析:根据点在二次函数图象上,则点的横纵坐标满足二次函数的解析式,把x=-1,y=0代入y=ax2-bx+c得到a+b+c=0,则b+c=-a,c+a=-b,a+b=-c,把它们分别代入所求的分式中即可得到分式的值.
解答:解:∵函数y=ax2-bx+c的图象过点(-1,0),即x=-1时,y=0,
∴a+b+c=0,
∴b+c=-a,c+a=-b,a+b=-c,
∴原式=
+
+
=-1-1-1
=-3.
故答案为-3.
∴a+b+c=0,
∴b+c=-a,c+a=-b,a+b=-c,
∴原式=
| a |
| -a |
| b |
| -b |
| c |
| -c |
=-1-1-1
=-3.
故答案为-3.
点评:本题考查了二次函数图象上点的坐标特征:点在二次函数图象上,则点的横纵坐标满足二次函数的解析式.也考查了分式的化简求值.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
 11、如图是函数y=ax2+bx+c图象的一部分,那么图象与x轴相交时右边交点的坐标是
11、如图是函数y=ax2+bx+c图象的一部分,那么图象与x轴相交时右边交点的坐标是
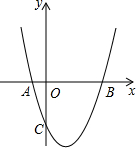 (2012•重庆模拟)如图,函数y=ax2+bx+c(c≠0)的图象与x轴交于A,B两点(A点在B点左侧),与y轴交于点C,若A点坐标(-1,0),若B点坐标(3,0),则下列说法正确的是( )
(2012•重庆模拟)如图,函数y=ax2+bx+c(c≠0)的图象与x轴交于A,B两点(A点在B点左侧),与y轴交于点C,若A点坐标(-1,0),若B点坐标(3,0),则下列说法正确的是( ) ,顶点为
,顶点为 .
.