题目内容
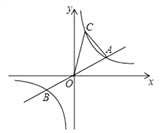
【题目】已知二次函数图象的顶点坐标为M(1,0),直线![]() 与该二次函数的图象交于A,B两点,其中A点的坐标为(3,-4),B点在y轴上.
与该二次函数的图象交于A,B两点,其中A点的坐标为(3,-4),B点在y轴上.
(1)求m的值及这个二次函数的解析式;
(2)在x轴上找一点Q,使△QAB的周长最小,并求出此时Q点坐标;
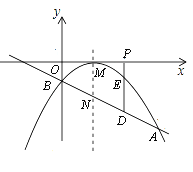
(3)若P(t,0)是x轴上的一个动点,过P作x轴的垂线分别与直线AB和二次函数的图象交于D、E两点.
①设线段DE的长为h,当0<t<3时,求h与t之间的函数关系式;
②若直线AB与抛物线的对称轴交点为N,问是否存在一点P,使以M、N、D、E为顶点的四边形是平行四边形?若存在,请求出此时P点的坐标;若不存在,请说明理由.
【答案】(1) ![]() ,m=-1;(2)
,m=-1;(2)![]() (
(![]() ,0);(3)①
,0);(3)①![]() ;
;
② 存在,理由见解析.
【解析】分析:(1)设抛物线的解析式为y=![]() ,将A点坐标分别代入抛物线和直线的解析式,即可求出抛物线的解析式和m的值;(2)使△QAB的周长最小,即是求AQ+BQ的值最小,作出B点关于x轴的对称点B′,当A、Q、B′三点在一条直线上时,△QAB的周长最小,求得直线AB'的解析式,即可求得点Q的坐标;(3)①根据P点坐标分别表示出D、E两点坐标,即可求出h与t之间的函数关系式;② 存在,分抛物线在直线上方时和抛物线在直线下方时两种情况求点P的坐标.
,将A点坐标分别代入抛物线和直线的解析式,即可求出抛物线的解析式和m的值;(2)使△QAB的周长最小,即是求AQ+BQ的值最小,作出B点关于x轴的对称点B′,当A、Q、B′三点在一条直线上时,△QAB的周长最小,求得直线AB'的解析式,即可求得点Q的坐标;(3)①根据P点坐标分别表示出D、E两点坐标,即可求出h与t之间的函数关系式;② 存在,分抛物线在直线上方时和抛物线在直线下方时两种情况求点P的坐标.
详解:
(1)∵二次函数图象的顶点M(1, 0), ∴二次函数可表达为y=![]()
又∵图象过A(3,-4),∴![]() =-4,解得a=-1,
=-4,解得a=-1,
∴二次函数解析式为: ![]() ,
,
A(3,- 4)在直线y = -x + m上:-3+m=-4,m=-1;
(2)由![]() 得B(0,-1),
得B(0,-1),
B关于x轴的对称点为B'(0, 1)
设直线AB'的解析式为:y=kx+1,将A(3,-4)代入得:-4=3k+1,解得k=-![]() ,
,
∴y=-![]() ,令y=0,得x=
,令y=0,得x=![]() ,
,
∴![]() (
(![]() ,0),此时A、Q、
,0),此时A、Q、![]() 在一条直线上,所以
在一条直线上,所以![]() ,
,
即△QAB的周长最小,![]() (
(![]() ,0),
,0),
(3)直线AB的解析式为:y=-x-1,抛物线为: ![]() ,
,
①∵0<t<3,∴h=-t+2t-1-(-t-1)=-t+3t ;
② 存在
∵ M(1,0)∴N(1,-2),∴MN=2, MN//DE,∴只要DE=MN=2即可
1)当抛物线在直线上方时,由-t+3t =2,解得t=1或t=2,
当t=1时MN与
2)当抛物线在直线下方时,由t+3t =2,解得![]() ,
,
此时![]() 和
和![]() ,综上所述P点共有:
,综上所述P点共有:
![]() ,
,![]() ,
,![]() 共三个
共三个