Question

【题目】如图，直线AB经过⊙O上的点C，并且OA=OB，CA=CB，⊙O交直线OB于E，D，交OA于点F，连接EF并延长EF交AB于G，且EG⊥AB．

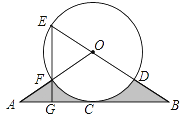
（1）求证：直线AB是⊙O的切线；

（2）若EF=2FG，AB= ，求图中阴影部分的面积；

（3）若EG=9，BG=12，求BD的长．

Answer 1

【答案】（1）详见解析；（2）；（3） ．

【解析】

（1）连接OE，由OA＝OB，CA＝CB，根据等腰三角形的性质得到OC⊥AB，根据切线的判定定理即可得到结论；

（2）过O点作OH⊥EG于H，则EH＝FH，由EF＝2FG，得到EHEG，又OH∥BG，根据平行线分线段成比例定理得到EH：EG＝EO：EB，BO＝2OE，则OB＝2OC，得到∠B＝30°，而BCAB＝6，利用含30°的直角三角形三边的关系得到OCBC＝6，然后根据三角形和扇形的面积公式利用S阴影部分＝S△OAB﹣S扇形OFD计算即可；

（3）利用勾股定理得到BE的长，设⊙O的半径为r，易证Rt△BOC∽Rt△BEG，由相似三角形的性质得到BCr，BOr，则15﹣rr，求出r，利用BD＝BE﹣ED计算即可．

（1）连接OC，如图，∵OA＝OB，CA＝CB，∴OC⊥AB，∴直线AB是⊙O的切线；

（2）过O点作OH⊥EG于H，如图，∵OE＝OF，∴EH＝FH．

∵EF＝2FG，∴EHEG，而EG⊥AB，∴OH∥BG，∴EH：EG＝EO：EB，∴BO＝2OE，∴OB＝2OC，∴∠B＝30°，∠COB＝60°．

而BCAB＝6，∴OCBC＝6，∴S阴影部分＝S△OAB﹣S扇形OFD126＝3612π；

（3）在Rt△BEG中，EG＝9，BG＝12，∴BE15，设⊙O的半径为r，则OB＝15﹣r．

∵OC∥EG，∴Rt△BOC∽Rt△BEG，∴OC：EG＝BC：BG＝BO：BE，即r：9＝BC：12＝BO：15，∴BCr，BOr，∴15﹣rr，解得：r，∴BD＝BE﹣ED＝15﹣2．