题目内容
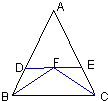25、阅读理解：“在一个三角形中，如果角相等，那么它们所对的边也相等．”简称“等角对等边”，如图，在△ABC中，已知∠ABC和∠ACB的平分线上交于点F，过点F作BC的平行线分别交AB、AC于点D、E，请你用“等角对等边”的知识说明DE=BD+CE．分析：由DE∥BC，BF平分∠ABC，CF平分∠ACB可知，DB=DF，CE=EF．便可得出结论．
解答：解：∵BF平分∠ABC（已知），CF平分∠ACB（已知），
∴∠ABF=∠CBF，∠ACF=∠FCB；
又∵DE平行BC（已知）
∴∠DFB=∠FBC（两直线平行，内错角相等），∠EFC=∠FCB（两直线平行，内错角相等），
∴∠DBF=∠DFB，∠EFC=∠ECF（等量代换）
∴DF=DB，EF=EC（等角对等边）
∴DE=BD+CE．
∴∠ABF=∠CBF，∠ACF=∠FCB；
又∵DE平行BC（已知）
∴∠DFB=∠FBC（两直线平行，内错角相等），∠EFC=∠FCB（两直线平行，内错角相等），
∴∠DBF=∠DFB，∠EFC=∠ECF（等量代换）
∴DF=DB，EF=EC（等角对等边）
∴DE=BD+CE．
点评：此题考查学生对等腰三角形的判定与性质和平行线的性质的理解和掌握，主要利用等腰三角形两边相等．稍微有点难度是一道中档题．
练习册系列答案
相关题目
的值．
