题目内容
 如图,四边形ABCD是正方形,点E、F分别在BC和CD上,且BE=DF=
如图,四边形ABCD是正方形,点E、F分别在BC和CD上,且BE=DF= AB.小松同学在作题时发现,当n=2时,sin∠EAF=
AB.小松同学在作题时发现,当n=2时,sin∠EAF= ,当n=3时,sin∠EAF=
,当n=3时,sin∠EAF= ,当n=4时,sin∠EAF=
,当n=4时,sin∠EAF=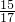 ,当n=5时,sin∠EAF=
,当n=5时,sin∠EAF= .
.
(1)当BE=DF= AB时,sin∠EAF=______.
AB时,sin∠EAF=______.
(2)证明你上面的结论.
解:(1)将各三角函数值排列出来,将 化为
化为 ,
,
从而观察可得出结论,当BE=DF= AB时,sin∠EAF=
AB时,sin∠EAF= .
.
(2)证明:设BE=1,则DF=1,CE=CF=n-1,

连接EF,作FM⊥AE于点M,
则S△AEF=S正方形ABCD-S△ABE-S△ADF-S△CEF,
=n2- ×1×n-
×1×n- ×1×n-
×1×n- ×(n-1)2
×(n-1)2
= (n2-1).
(n2-1).
在Rt△AFM中,FM=AF•sin∠EAF,AE=AF=
∴S=(1+n2)sin∠EAF
∴ (1+n2)sin∠EAF=
(1+n2)sin∠EAF= (n2-1)
(n2-1)
∴sin∠EAF= .
.
分析:(1)将将 化为
化为 ,根据分子及分母的特点可得出当BE=DF=
,根据分子及分母的特点可得出当BE=DF= AB时,sin∠EAF的值.
AB时,sin∠EAF的值.
(2)设BE=1,则DF=1,CE=CF=n-1,先根据S△AEF=S正方形ABCD-S△ABE-S△ADF-S△CEF求出一个值,然后在Rt△AFM中在表示出一个值,两者相等即可得出结论.
点评:此题考查了正方形的性质、勾股定理及锐角三角函数的定义,属于规律型,难度较大,解答本题的关键是仔细观察题目所给三角函数值的特点,从而得出结论,这样题目就变得简单化.
 化为
化为 ,
,从而观察可得出结论,当BE=DF=
 AB时,sin∠EAF=
AB时,sin∠EAF= .
.(2)证明:设BE=1,则DF=1,CE=CF=n-1,

连接EF,作FM⊥AE于点M,
则S△AEF=S正方形ABCD-S△ABE-S△ADF-S△CEF,
=n2-
 ×1×n-
×1×n- ×1×n-
×1×n- ×(n-1)2
×(n-1)2=
 (n2-1).
(n2-1).在Rt△AFM中,FM=AF•sin∠EAF,AE=AF=

∴S=(1+n2)sin∠EAF
∴
 (1+n2)sin∠EAF=
(1+n2)sin∠EAF= (n2-1)
(n2-1)∴sin∠EAF=
 .
.分析:(1)将将
 化为
化为 ,根据分子及分母的特点可得出当BE=DF=
,根据分子及分母的特点可得出当BE=DF= AB时,sin∠EAF的值.
AB时,sin∠EAF的值.(2)设BE=1,则DF=1,CE=CF=n-1,先根据S△AEF=S正方形ABCD-S△ABE-S△ADF-S△CEF求出一个值,然后在Rt△AFM中在表示出一个值,两者相等即可得出结论.
点评:此题考查了正方形的性质、勾股定理及锐角三角函数的定义,属于规律型,难度较大,解答本题的关键是仔细观察题目所给三角函数值的特点,从而得出结论,这样题目就变得简单化.

练习册系列答案
相关题目
 如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条)
如图,四边形ABCD的对角线AC与BD互相垂直平分于点O,设AC=2a,BD=2b,请推导这个四边形的性质.(至少3条) 如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF.
如图,四边形ABCD的对角线AC、BD交于点P,过点P作直线交AD于点E,交BC于点F.若PE=PF,且AP+AE=CP+CF. 如图,四边形ABCD,AB=AD=2,BC=3,CD=1,∠A=90°,求∠ADC的度数.
如图,四边形ABCD,AB=AD=2,BC=3,CD=1,∠A=90°,求∠ADC的度数. 如图,四边形ABCD为正方形,E是BC的延长线上的一点,且AC=CE,求∠DAE的度数.
如图,四边形ABCD为正方形,E是BC的延长线上的一点,且AC=CE,求∠DAE的度数.