题目内容
【题目】如图,一次函数![]() 的图象与
的图象与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,在
两点,在![]() 轴上有一点
轴上有一点![]() ,动点
,动点![]() 从
从![]() 点以每秒2个单位长度的速度向左移动,
点以每秒2个单位长度的速度向左移动,
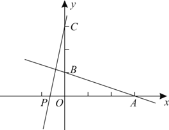
(1)求直线![]() 的表达式;
的表达式;
(2)求![]() 的面积
的面积![]() 与移动时间
与移动时间![]() 之间的函数关系式;
之间的函数关系式;
(3)当![]() 为何值时,
为何值时,![]() ≌
≌![]() ,求出此时
,求出此时![]() 点的坐标.
点的坐标.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() ;当
;当![]() 时
时![]() (3) 当
(3) 当![]() 时,P的坐标为
时,P的坐标为![]() ;当
;当![]() 时,P的坐标为
时,P的坐标为![]()
【解析】
(1)将A,B点代入用待定系数法即可求解;
(2)先计算出P点到达原点的时间,然后以此为分界线,分情况讨论即可;
(3)根据全等的性质可得出![]() ,然后分P在原点的左右两侧两种情况讨论即可求出P点坐标.
,然后分P在原点的左右两侧两种情况讨论即可求出P点坐标.
解(1)设直线AB的表达式为![]()
将![]() ,
,![]() 两点代入得
两点代入得
![]() 解得
解得 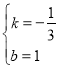
∴AB的表达式为![]()
(2)![]()
当![]() 时
时
![]()
当![]() 时
时
![]()
(3)若![]() ≌
≌![]() 时
时![]()
![]()
![]()
![]()
当![]() 时,
时,![]() ,此时P的坐标为
,此时P的坐标为![]() ;
;
当![]() 时,
时,![]() ,此时P的坐标为
,此时P的坐标为![]() ;
;

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目