题目内容
| x | … | -1 | 0 | 1 | 3 | … |
| y | … | -3 | 1 | 3 | 1 | … |
④
分析:先根据表中x=0时,y=1;x=-1时,y=-3;x=1时,y=3代入二次函数y=ax2+bx+c的解析式,再根据二次函数的性质对各小题进行逐一分析.
解答:∵x=0时,y=1;x=-1时,y=-3;x=1时,y=3代入二次函数y=ax2+bx+c的解析式得,
 ,解得
,解得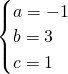 ,
,
∴此二次函数的解析式为:y=-x2+3x+1,
∵a=-1<0,
∴此抛物线开口向下,故①错误;
∵c=1>0,
∴抛物线与y轴交于正半轴,故②错误;
∵当x=4时,y=-42+3×4+1=-3<0,故③错误;
令-x2+3x+1=0,则x= ,
,
∴方程的正根为x= =
= ,
,
∵3< <4,
<4,
∴3+3<3+ <3+4,
<3+4,
∴3< <3.5,
<3.5,
∴方程ax2+bx+c=0的正根在3与4之间,故④正确.
故答案为④.
点评:本题考查的是抛物线与x轴的交点,能根据题意得出抛物线的解析式是解答此题的关键.
分析:先根据表中x=0时,y=1;x=-1时,y=-3;x=1时,y=3代入二次函数y=ax2+bx+c的解析式,再根据二次函数的性质对各小题进行逐一分析.
解答:∵x=0时,y=1;x=-1时,y=-3;x=1时,y=3代入二次函数y=ax2+bx+c的解析式得,
 ,解得
,解得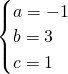 ,
,∴此二次函数的解析式为:y=-x2+3x+1,
∵a=-1<0,
∴此抛物线开口向下,故①错误;
∵c=1>0,
∴抛物线与y轴交于正半轴,故②错误;
∵当x=4时,y=-42+3×4+1=-3<0,故③错误;
令-x2+3x+1=0,则x=
 ,
,∴方程的正根为x=
 =
= ,
,∵3<
 <4,
<4,∴3+3<3+
 <3+4,
<3+4,∴3<
 <3.5,
<3.5,∴方程ax2+bx+c=0的正根在3与4之间,故④正确.
故答案为④.
点评:本题考查的是抛物线与x轴的交点,能根据题意得出抛物线的解析式是解答此题的关键.

练习册系列答案
相关题目