题目内容
 如图,以△ABC的边AB、AC向外作等边△ABE和△ACD,连接BD、CE.
如图,以△ABC的边AB、AC向外作等边△ABE和△ACD,连接BD、CE.(1)线段CE和BD有什么数量关系?证明你的结论.
(2)能否求出∠DFC的度数?
分析:(1)由等边三角形的性质,不难看出CE与BD之间的关系,即求解△ABD与△ACE全等即可;
(2)由(1)△ABD与△ACE可得∠ADG=∠FCG,又∠AGD=∠FGC,从而得∠DFC=∠DAC=60°.
(2)由(1)△ABD与△ACE可得∠ADG=∠FCG,又∠AGD=∠FGC,从而得∠DFC=∠DAC=60°.
解答:解:(1)CE=BD;
证明如下:
∵△ABE和△ACD是等边三角形,
∴AB=AE,AD=AC,∠BAE=∠CAD=60°,
∴∠BAE+∠BAC=∠CAD+∠BAC,
即∠CAE=∠BAD,
∴△ABD≌△ACE(SAS),
∴CE=BD;
(2)∵△ABD与△ACE(已证),
∴∠ADG=∠FCG,
又∠AGD=∠FGC,
∴∠DFC=∠DAC=60°.
证明如下:
∵△ABE和△ACD是等边三角形,
∴AB=AE,AD=AC,∠BAE=∠CAD=60°,
∴∠BAE+∠BAC=∠CAD+∠BAC,
即∠CAE=∠BAD,
∴△ABD≌△ACE(SAS),
∴CE=BD;
(2)∵△ABD与△ACE(已证),
∴∠ADG=∠FCG,
又∠AGD=∠FGC,
∴∠DFC=∠DAC=60°.
点评:本题考查了全等三角形的判定与性质及等边三角形的性质;可围绕结论寻找全等三角形,运用全等三角形的性质判定线段相等,证得∠CAE=∠BAC是正确解答本题的关键.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
 26、如图,以△ABC的边AB、AC为边的等边三角ABD和等边三角形ACE,四边形ADFE是平行四边形.
26、如图,以△ABC的边AB、AC为边的等边三角ABD和等边三角形ACE,四边形ADFE是平行四边形.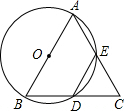 如图,以△ABC的边AB为直径作⊙O,交BC于D点,交AC于E点,BD=DE
如图,以△ABC的边AB为直径作⊙O,交BC于D点,交AC于E点,BD=DE
 (2011•峨眉山市二模)如图,以△ABC的边AB为直径作⊙O,BC与⊙O交于D,D是BC的中点,过D作DE⊥AC,交AC于点E.
(2011•峨眉山市二模)如图,以△ABC的边AB为直径作⊙O,BC与⊙O交于D,D是BC的中点,过D作DE⊥AC,交AC于点E. (2010•黔东南州)如图,以△ABC的边BC为直径作⊙O分别交AB,AC于点F.点E,AD⊥BC于D,AD交于⊙O于M,交BE于H.
(2010•黔东南州)如图,以△ABC的边BC为直径作⊙O分别交AB,AC于点F.点E,AD⊥BC于D,AD交于⊙O于M,交BE于H.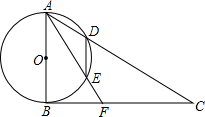 如图,以△ABC的边AB为直径的⊙O交AC于点D,弦DE∥AB,∠C=∠BAF
如图,以△ABC的边AB为直径的⊙O交AC于点D,弦DE∥AB,∠C=∠BAF