题目内容
已知四边形ABCD(不是平行四边形)中,AD与BC不平行,E、F、G、H分别是线段AB、AC、CD、BD的中点.(1)证明:四边形EFGH是平行四边形;
(2)图中不再添加其它的点和线,根据现有条件,在空格内分别添加一个你认为正确的条件,使下列命题成立:
①当四边形ABCD满足条件______时,四边形EFGH是菱形;
②当四边形ABCD满足条件______时,四边形EFGH是矩形.

【答案】分析:(1)根据一组对边平行且相等的四边形是平行四边形.只需证EH∥FG,EH=FG即可.
(2)根据一组邻边相等的平行四边形是菱形.只需证EH=HG,由中位线定理可证EH= AD,HG=
AD,HG= BC,
BC,
所以AD=BC.
(3)根据有一个角是直角的平行四边形是矩形.只需证∠EHG=90°,必须AD⊥BC.
解答:解:(1)∵E、F、G、H分别是线段AB、AC、CD、BD的中点,
∴EH、FG分别是△ABD、△ACD的中位线,
∴EH∥AD,FG∥AD,EH= AD,FG=
AD,FG= AD,
AD,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形.
(2)AD=BC;
∵EH、HG分别是△ABD、△BCD的中位线,
∴EH= AD,HG=
AD,HG= BC,
BC,
∵AD=BC,
∴EH=HG,
∴平行四边形EFGH是菱形.
(3)AD⊥BC.
∵EH、HG分别是△ABD、△BCD的中位线,
∴EH∥AD,HG∥BC,
∵AD⊥BC,
∴EH⊥HG,∠EHG=90°
∴平行四边形EFGH是矩形.
点评:本题利用了:
1、三角形中位线的性质;
2、平行四边形的判定;
3、一组邻边相等的平行四边形是菱形;
4、有一个角是直角的平行四边形是矩形.
(2)根据一组邻边相等的平行四边形是菱形.只需证EH=HG,由中位线定理可证EH=
 AD,HG=
AD,HG= BC,
BC,所以AD=BC.
(3)根据有一个角是直角的平行四边形是矩形.只需证∠EHG=90°,必须AD⊥BC.
解答:解:(1)∵E、F、G、H分别是线段AB、AC、CD、BD的中点,
∴EH、FG分别是△ABD、△ACD的中位线,
∴EH∥AD,FG∥AD,EH=
 AD,FG=
AD,FG= AD,
AD,∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形.
(2)AD=BC;
∵EH、HG分别是△ABD、△BCD的中位线,
∴EH=
 AD,HG=
AD,HG= BC,
BC,∵AD=BC,
∴EH=HG,
∴平行四边形EFGH是菱形.
(3)AD⊥BC.
∵EH、HG分别是△ABD、△BCD的中位线,
∴EH∥AD,HG∥BC,
∵AD⊥BC,
∴EH⊥HG,∠EHG=90°
∴平行四边形EFGH是矩形.
点评:本题利用了:
1、三角形中位线的性质;
2、平行四边形的判定;
3、一组邻边相等的平行四边形是菱形;
4、有一个角是直角的平行四边形是矩形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
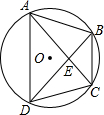 如图,已知四边形ABCD是⊙O的内接四边形,且AB=CD=5,AC=7,BE=3.下列命题错误的是( )
如图,已知四边形ABCD是⊙O的内接四边形,且AB=CD=5,AC=7,BE=3.下列命题错误的是( )| A、△ABE≌△DCE | B、∠BDA=45° | C、S四边形ABCD=24.5 | D、图中全等的三角形共有2对 |
如图,已知四边形ABCD是边长为2的正方形,E是AB的中点,F是BC的中点,AF与DE相交于G,BD和AF相交于H,那么四边形BEGH的面积是( )

A、
| ||
B、
| ||
C、
| ||
D、
|
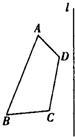 32、如图,已知四边形ABCD和直线L.
32、如图,已知四边形ABCD和直线L.