Question

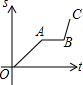
如图，边长为2的等边三角形△ABC中，BC⊥x轴，C点坐标（

3

，-

1

2

），则点A的坐标是

 

．

Answer 1

考点：等边三角形的性质,坐标与图形性质

专题：

分析：过A作AD⊥BC于D，根据等边三角形性质得出AB=AC，根据三线合一定理求出CD，即可求出OA，即可得出答案．

解答：解：
过A作AD⊥BC于D，
∵△ABD是等边三角形，
∴AB=AC，
∴BD=DC=

1

2

BC=1，
∵BC⊥x轴，C点坐标（

3

，-

1

2

），
∴OA=1-

1

2

=

1

2

，
即A的坐标是（0，

1

2

），
故答案为：（0，

1

2

）．

点评：本题考查了坐标与图形性质，等边三角形性质，等腰三角形的性质的应用，关键是求出CD长．