题目内容
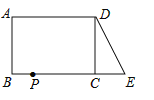
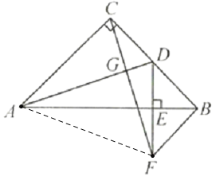
【题目】已知：如图，在等腰直角三角形
中，
，
为
的中点，且
，垂足为点
，过点
作
交
的延长线于点
，联结
.
（1）求证：
；
（2）连接
，试判断
的形状，并说明理由.
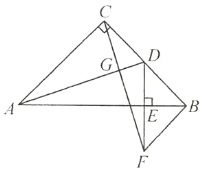
【答案】（1）见解析；（2）
是等腰三角形，理由见解析.
【解析】
（1）由
和
证明△DBF=等腰直角三角形，再证明
，得
，从而证明
；
（2）证明
，可得
，再由（1）知
，从而证明
，即可说明△ACF的性质.
（1）证明：
，，
，
∵
，
∴∠FEB=90°，
∴∠BFE=45°，
∴△DBF=等腰直角三角形，
∴DB=BF，
∵
为
的中点，
∴DC=BD，
∴DC=FB，
在△ACD和△CBF中
，
，
，
；
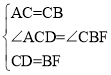
（2）连接
，
由（1）知△DBF等腰直角三角形，
，
∴DE=FE，
在△ADE和△AFE中
，
，
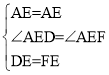
由（1）知，
，
，
是等腰三角形.
练习册系列答案
步步高达标卷系列答案
相关题目
