Question

如图①，在平面直角坐标系中，已知A（6，6）、B（12，O）、M（3，0），∠MAN=45゜．
（1）判断△AOB的形状为______；
（2）求线段AN的长；
（3）如图②，若C（-3，O），在y 轴的负半轴上是否存在一点P，使∠NPO=2∠CPO？若存在，求点P的坐标；若不存在，请说明理由．

Answer 1

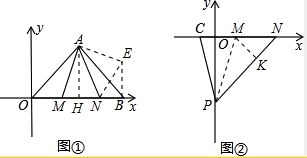解：（1）过点A作AH⊥OB，垂足为H，
∵A（6，6），
∴OH=6，
∵B（12，O），
∴HB=6，
∴AO=AB，
∵∠MAN=45゜，
∴∠ABO=45°，
∴∠OAB=90°，
∴△AOB的形状为等腰直角三角形；
故答案为：等腰直角三角形；
（2）作∠NAE=∠NAM=45°，使点E与M在AN两侧，连接BE，NE，使AE=AM，
∵∠MAE=∠OAB=90°，
∴∠BAE=∠OAM，
∵AB=AO，
∴△BAE≌△OAM，
∴BE=OM=3，NE=MN，∠ABE=∠AOM=45°，
∴∠NBE=90°，
∴BN²+BE²=NE²，
设BN=x，则NE=MN=OB-OM-NB=12-x-3=9-x，
∴x²+3²=（9-x）²，
∴x=4，
∴ON=8，
∴HN=ON-OH=8-6=2，
∴AN=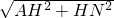==2；
（3）连接PM，作MK垂直PN于K，
∵OM=OC=3，
∴PO垂直平分CM，
∴PC=PM，∠MPO=∠CPO，
∵∠NPO=2∠CPO，
∴∠NPO=2∠MPO，
∴∠NPM=∠MPO，
∴MK=MO=3，
∵S_△NPM：S_△MPO=PN：PO，
S_△NPM：S_△MPO=NM：OM=5：3，
∴PN：PO=NM：OM=5：3，
设PN=5t，
则PO=3t，
则8²+（3t）²=（5t）²，
解得：t=2，
则OP=6，
则点P为（0，-6）．
分析：（1）过点A作AH⊥OB，垂足为H，求出OH=6，HB=6，AO=AB，再根据∠MAN=45゜，∠ABO=45°，得出∠OAB=90°，即可判断出△AOB的形状为等腰直角三角形；
（2）作∠NAE=∠NAM=45°，使点E与M在AN两侧，连接BE，NE，使AE=AM，先证出△BAE≌△OAM，得出BE=OM=3，NE=MN，∠ABE=∠AOM=45°，∠NBE=90°，BN²+BE²=NE²，再设BN=x，则NE=9-x，从而得出x²+3²=（9-x）²，最后根据AN=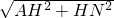代入计算即可；
（3）连接PM，作MK垂直PN于K，则PO垂直平分CM，得出PC=PM，∠MPO=∠CPO，再证出∠NPM=∠MPO，则MK=MO=3，再根据S_△NPM：S_△MPO=PN：PO=NM：OM=5：3，设PN=5t，则PO=3t，
得出8²+（3t）²=（5t）²，求出t的值即可得出点P的坐标．
点评：此题考查了等腰直角三角形、勾股定理，用到的知识点是等腰直角三角形的判定与性质，勾股定理，角平分线的性质，关键是运用有关性质和定理，求出线段的长度，得出点的坐标．