题目内容
 已知:AB⊥BC于B,CD⊥BC于C,AB=4,CD=6,BC=14,P为BC上一点,试问BP=
已知:AB⊥BC于B,CD⊥BC于C,AB=4,CD=6,BC=14,P为BC上一点,试问BP=分析:本题主要应用两三角形相似的判定定理,做题即可.
解答:解:∵AB⊥DB,CD⊥DB,
∴∠C=∠B=90°,设BP=x,
当PB:DC=AB:PC时,△PAB∽△DPC,
∴
=
,
∴x=2或12;
当PB:PC=AB:DC时,△PAB∽△PDC,
∴
=
,
解得:x=5.6;
解得BP=2或12或5.6.
故答案为:2或12或5.6.
∴∠C=∠B=90°,设BP=x,
当PB:DC=AB:PC时,△PAB∽△DPC,
∴
| x |
| 6 |
| 4 |
| 14-x |
∴x=2或12;
当PB:PC=AB:DC时,△PAB∽△PDC,
∴
| x |
| 14-x |
| 4 |
| 6 |
解得:x=5.6;
解得BP=2或12或5.6.
故答案为:2或12或5.6.
点评:此题考查了相似三角形的判定,①如果两个三角形的三组对应边的比相等,那么这两个三角形相似;②如果两个三角形的两条对应边的比相等,且夹角相等,那么这两个三角形相似;③如果两个三角形的两个对应角相等,那么这两个三角形相似.平行于三角形一边的直线截另两边或另两边的延长线所组成的三角形与原三角形相似.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
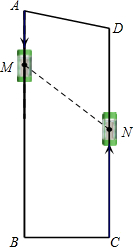 (2011•安宁市一模)随着科学技术的不断发展,人们的出行购物将会变得便捷、轻松,下图是我市未来购物商场的两部电梯的抽象图.已知:AB⊥BC于B,DC⊥BC于C,AB=26米,DC=24米,BC=8米.电梯M从A出发以1米/秒的速度匀速向下移动,同时,电梯N从C出发以2米/秒的速度匀速向上移动.因电梯还处在测试阶段,测试人员为了很好地测试电梯,规定当一个电梯到达另一个端点时,两部电梯停止移动.设电梯移动时间为t秒,请你帮测试人员先算一算:
(2011•安宁市一模)随着科学技术的不断发展,人们的出行购物将会变得便捷、轻松,下图是我市未来购物商场的两部电梯的抽象图.已知:AB⊥BC于B,DC⊥BC于C,AB=26米,DC=24米,BC=8米.电梯M从A出发以1米/秒的速度匀速向下移动,同时,电梯N从C出发以2米/秒的速度匀速向上移动.因电梯还处在测试阶段,测试人员为了很好地测试电梯,规定当一个电梯到达另一个端点时,两部电梯停止移动.设电梯移动时间为t秒,请你帮测试人员先算一算: 如图,已知:AB⊥BC于B,EF⊥AC于G,DF⊥BC于D,BC=DF.求证:AC=EF.
如图,已知:AB⊥BC于B,EF⊥AC于G,DF⊥BC于D,BC=DF.求证:AC=EF.
