题目内容
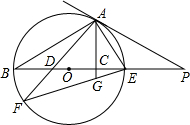 (2013•竹溪县模拟)如图BE是⊙O的直径,点A是⊙O上一点,连结AE,延长BE至点P,连结PA,∠PAE=∠ABE,过点A作AC⊥BE于点C,点D是BO上一点,直线AD交⊙O于点F,连结FE与直线AC交于点G.
(2013•竹溪县模拟)如图BE是⊙O的直径,点A是⊙O上一点,连结AE,延长BE至点P,连结PA,∠PAE=∠ABE,过点A作AC⊥BE于点C,点D是BO上一点,直线AD交⊙O于点F,连结FE与直线AC交于点G.(1)直线PA是否为⊙O的切线,并证明你的结论;
(2)若PE=4,tan∠EAC=
| 1 | 2 |
(3)求证:AE2=EG•EF.
分析:(1)连接OA,根据等腰三角形性质和已知求出∠ABE=∠BAO=∠PAE,求出∠BAE=∠PAO=90°,根据切线判定推出即可.
(2)设CE=x,AC=2x,证△ACB∽△ECA,求出BC=4x,求出OA=OE=2.5x,在Rt△PAO和Rt△PCA中,由勾股定理得出PA2=PC2+AC2=PO2-OA2,得出方程,求出x即可.
(3)求出∠EAC=∠AFE,∠AEF=∠AEG,推出△EAG∽∠EFA,得出
=
,即可得出答案.
(2)设CE=x,AC=2x,证△ACB∽△ECA,求出BC=4x,求出OA=OE=2.5x,在Rt△PAO和Rt△PCA中,由勾股定理得出PA2=PC2+AC2=PO2-OA2,得出方程,求出x即可.
(3)求出∠EAC=∠AFE,∠AEF=∠AEG,推出△EAG∽∠EFA,得出
| AE |
| EG |
| EF |
| AE |
解答:(1)直线PA为⊙O的切线,
证明:连接OA,
∵OA=OB,
∴∠ABE=∠BAO,
∵∠PAE=∠ABE,
∴∠PAE=∠BAO,
∴∠PAE+∠OAE=∠BAO+∠OAE,
∴∠BAE=∠PAO,
∵BE是⊙O直径,
∴∠BAE=90°,
∴∠PAO=90°,
∴OA⊥PA,
∵OA为半径,
∴直线PA为⊙O的切线;
(2)解:∵AC⊥BE,
∴tan∠EAC=
=
,
∴设CE=x,AC=2x,
∵AC⊥BE,∠BAE=90°,
∴∠ACE=∠BAE=90°,
∴∠BAC+∠EAC=90°,∠EAC+∠AEC=90°,
∴∠BAC=∠AEC,
∵∠ACE=∠ACB=90°,
∴△ACB∽△ECA,
∴
=
,
∵CE=x,AC=2x,
∴BC=4x,
∴BE=x+4x=5x,
∴OA=OE=2.5x,
∵在Rt△PAO和Rt△PCA中,∠ACP=∠PAO=90°,由勾股定理得:PA2=PC2+AC2=PO2-OA2,
∴(4+x)2+(2x)2=(4+2.5x)2-(2.5x)2,
5x2-12x=0,
x1=0(舍去),x2=
,
∴OA=2.5x=2.5×
=6,
即⊙O的半径的长是6;
(3)证明:∵AC⊥BE,
∴∠BAE=∠ACE=90°,
∴∠EAC+∠AEC=90°,∠ABE+∠AEC=90°,
∴∠ABE=∠EAC,
∵∠ABE=∠AFE,
∴∠EAC=∠AFE,
∵∠AEF=∠AEG,
∴△EAG∽∠EFA,
∴
=
,
∴AE2=EG•EF.

证明:连接OA,
∵OA=OB,
∴∠ABE=∠BAO,
∵∠PAE=∠ABE,
∴∠PAE=∠BAO,
∴∠PAE+∠OAE=∠BAO+∠OAE,
∴∠BAE=∠PAO,
∵BE是⊙O直径,
∴∠BAE=90°,
∴∠PAO=90°,
∴OA⊥PA,
∵OA为半径,
∴直线PA为⊙O的切线;
(2)解:∵AC⊥BE,
∴tan∠EAC=
| 1 |
| 2 |
| CE |
| AC |
∴设CE=x,AC=2x,
∵AC⊥BE,∠BAE=90°,
∴∠ACE=∠BAE=90°,
∴∠BAC+∠EAC=90°,∠EAC+∠AEC=90°,
∴∠BAC=∠AEC,
∵∠ACE=∠ACB=90°,
∴△ACB∽△ECA,
∴
| AC |
| BC |
| CE |
| AC |
∵CE=x,AC=2x,
∴BC=4x,
∴BE=x+4x=5x,
∴OA=OE=2.5x,
∵在Rt△PAO和Rt△PCA中,∠ACP=∠PAO=90°,由勾股定理得:PA2=PC2+AC2=PO2-OA2,
∴(4+x)2+(2x)2=(4+2.5x)2-(2.5x)2,
5x2-12x=0,
x1=0(舍去),x2=
| 12 |
| 5 |
∴OA=2.5x=2.5×
| 12 |
| 5 |
即⊙O的半径的长是6;
(3)证明:∵AC⊥BE,
∴∠BAE=∠ACE=90°,
∴∠EAC+∠AEC=90°,∠ABE+∠AEC=90°,
∴∠ABE=∠EAC,
∵∠ABE=∠AFE,
∴∠EAC=∠AFE,
∵∠AEF=∠AEG,
∴△EAG∽∠EFA,
∴
| AE |
| EG |
| EF |
| AE |
∴AE2=EG•EF.
点评:本题考查了切线的性质和判定,等腰三角形的性质,解直角三角形,勾股定理,三角形的内角和定理的应用,主要考查学生综合运用性质进行推理和计算的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2013•竹溪县模拟)如图是二次函数y=ax2+bx+c(a≠0)在平面直角坐标系中的图象,根据图形判断:
(2013•竹溪县模拟)如图是二次函数y=ax2+bx+c(a≠0)在平面直角坐标系中的图象,根据图形判断: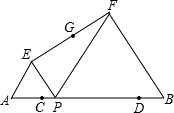 (2013•竹溪县模拟)如图:已知AB=10,点C、D在线段AB上且AC=DB=1; P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作等边△AEP和等边△PFB,连结EF,设EF的中点为G;当点P从点C运动到点D时,则点G移动路径的长是
(2013•竹溪县模拟)如图:已知AB=10,点C、D在线段AB上且AC=DB=1; P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作等边△AEP和等边△PFB,连结EF,设EF的中点为G;当点P从点C运动到点D时,则点G移动路径的长是