题目内容
已知：如图，AD=4，CD=3，∠ADC=90°，AB=13，BC=12．求图形的面积．
解：连接AC，在Rt△ACD中，AD=4，CD=3，
∴AC=
=5，
在△ABC中，
∵AC2+BC2=52+122=132=AB2，
∴△ABC为直角三角形；
∴图形面积为：
S△ABC-S△ACD=
×5×12-×3×4=24．
分析：连接AC，在Rt△ACD中，AD=4，CD=3，可求AC；在△ABC中，由勾股定理的逆定理可证△ABC为直角三角形，利用两个直角三角形的面积差求图形的面积．
点评：本题考查了勾股定理及其逆定理的运用，三角形面积的求法．
∴AC=
=5，在△ABC中，
∵AC2+BC2=52+122=132=AB2，
∴△ABC为直角三角形；
∴图形面积为：
S△ABC-S△ACD=
×5×12-×3×4=24．分析：连接AC，在Rt△ACD中，AD=4，CD=3，可求AC；在△ABC中，由勾股定理的逆定理可证△ABC为直角三角形，利用两个直角三角形的面积差求图形的面积．
点评：本题考查了勾股定理及其逆定理的运用，三角形面积的求法．
练习册系列答案
相关题目
27、已知：如图，AD∥BC，ED∥BF，且AF=CE．
25、已知，如图，AD∥BC，∠1=∠2，∠A=120°，且BD⊥CD，求∠C的度数．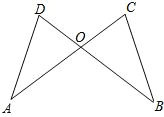
已知：如图，AD=BC，AC=BD．试判断OD、OC的数量关系，并说明理由．
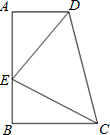已知，如图，AD∥BC，∠A=90°，AD=BE，∠EDC=∠ECD，请你说明下列结论成立的理由：（1）△AED≌△BCE，（2）AB=AD+BC．
根据题意填空：