Question

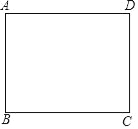
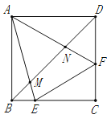
【题目】如图，正方形中，点分别在线段上运动，且满足，分别与相交于点，下列说法中：①；②点到线段的距离一定等于正方形的边长；③若，则；④若，，则．其中结论正确的是___________；（将正确的序号填写在横线上）

Answer 1

【答案】①②③④

【解析】

如图，根据旋转的性质得到BH=DF，AH=AF，∠BAH=∠DAF，得到∠EAH=∠EAF=45°，根据全等三角形的性质得到EH=EF，∠AEB=∠AEF，于是得到BE+BH=BE+DF=EF，故①正确；过A作AG⊥EF于G，根据全等三角形的性质得到AB=AG，于是得到点A到线段EF的距离一定等于正方形的边长；故②正确；根据三角函数的定义设BE=m，AB=2m，求得CE=m，设DF=x，则CF=2m-x，EF=BE+DF=m+x，根据勾股定理得到x=m，于是得到tan∠DAF= ；故③正确；求得EF=BE+DF=5，设BC=CD=n，根据勾股定理即可得到结论．

如图，把△ADF绕点A顺时针旋转90°得到△ABH，

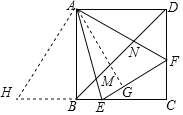
由旋转的性质得，BH=DF，AH=AF，∠BAH=∠DAF，

∵∠EAF=45°，

∴∠EAH=∠BAH+∠BAE=∠DAF+∠BAE=90°-∠EAF=45°，

∴∠EAH=∠EAF=45°，

在△AEF和△AEH中

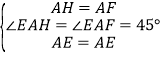
∴△AEF≌△AEH（SAS），

∴EH=EF，

∴∠AEB=∠AEF，

∴BE+BH=BE+DF=EF，

故①正确；

过A作AG⊥EF于G，

∴∠AGE=∠ABE=90°，

在△ABE与△AGE中

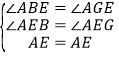
∴△ABE≌△AGE（AAS），

∴AB=AG，

∴点A到线段EF的距离一定等于正方形的边长；故②正确；

∵tan∠BAE==，

∴设BE=m，AB=2m，

∴CE=m，

设DF=x，则CF=2m-x，EF=BE+DF=m+x，

∵CF2+CE2=EF2，

∴（2m-x）2+m2=（m+x）2，

∴x=m，

∴tan∠DAF=；故③正确；

∵BE=2，DF=3，

∴EF=BE+DF=5，

设BC=CD=n，

∴CE=n-2，CF=n-3，

∴EF2=CE2+CF2，

∴25=（n-2）2+（n-3）2，

∴n=6（负值舍去），

∴AG=6，

∴S△AEF=×6×5=15．故④正确，

故答案为：①②③④．