Question

28． (本题12分)如图，一抛物线的顶点A为(2，－1)，交x轴于B、C(B左C右)两点，交y轴于点D，且B(1，0)，坐标原点为O，

(1)求抛物线解析式．

(2)连接CＤ、BD，在x轴上确定点E，使以A、C、E为顶点的三角形与△CBD相似，并求出点E的坐标．

(3)若点M(m，1)是抛物线上对称轴右侧的一点，点Q也在抛物线上，点P在x轴上，是否存在以O、M、P、Q为顶点的四边形是平行四边形，若存在，请直接写出点P的坐标；若不存在，请说明理由．

 

Answer 1

        E      

 P点坐标为（-4，0）；（4，0）；（4+，0）．

解析:解：（1）∵抛物线的顶点A为（2，-1），可设抛物线解析式为y=a（x-2）²-1，

把B（1，0）代入得，a-1=0，解得a=1，

∴y（x-2）²-1=x²-4x+3；

（2）令x=0，得y=3，∴D点坐标为（0，3）；

令y=0，得x²-4x+3=0，解得x₁=1，x₂=3，∴C点坐标为（3，0）；

过A作AH⊥x轴，如图，

易得△ODC和△ACH都为等腰直角三角形，BC=2，DC=3，AC=，

∴∠DCB=∠ACH=45°，

当以A、C、E为顶点的三角形与△CBD相似，则∠DCB=∠ACE=45°，

若CE：CB=CA：CD，即CE：2=：3，解得CE=，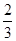

∴OE=3-=，则E点坐标为（，0）；

若CE：CD=CA：CB，即CE：3=：2，解得CE=3，

∴OE=3-3=0，则E点坐标为（0，0）舍去；

（3）存在．P点坐标为（-4，0）；（4，0）；（4+，0）．

 先确定M（2+，1），然后分类讨论：当OP为对角线，则M与Q到x轴的距离相等，都为1，所以Q点在A点，求出AM的解析式，得到与x轴的交点G的坐标，P1与O关于G对称，可得P1坐标；当OM为对角线，则MQ∥x轴，这样可确定Q2的坐标，然后利用平行四边形的性质可确定P2的坐标；同理可得到P3的坐标．