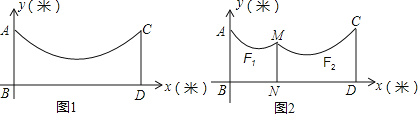��Ŀ����
����Ŀ�����������![]() �Ķ����ڒ�����
�Ķ����ڒ�����![]() �ϣ�������
�ϣ�������![]() �Ķ���Ҳ�ڒ�����
�Ķ���Ҳ�ڒ�����![]() ��ʱ����ô���dz�������
��ʱ����ô���dz�������![]() ��
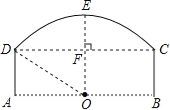
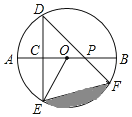
��![]() ����Ϊ�������������ߣ���ͼ1����֪������
����Ϊ�������������ߣ���ͼ1����֪������![]() ��
��![]() ��
��![]() ��
��![]() ������Ϊ�������Ē����ߣ���
������Ϊ�������Ē����ߣ���![]() �ֱ���������
�ֱ���������![]() ��
��![]() �Ķ��㣬������
�Ķ��㣬������![]() ������
������![]() ��
��
��1��ֱ��д��![]() �������������
�������������![]() �Ľ���ʽ��
�Ľ���ʽ��
��2��������![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() ��ֱ�������Σ�������ڣ��������E�����ꣻ��������ڣ���˵�����ɣ�
��ֱ�������Σ�������ڣ��������E�����ꣻ��������ڣ���˵�����ɣ�
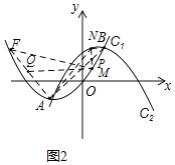
��3����ͼ2����![]() ��������
��������![]() �ϣ���
�ϣ���![]() �ֱ���������
�ֱ���������![]() ��
��![]() �ϵĶ��㣬�ҵ�
�ϵĶ��㣬�ҵ�![]() �ĺ�������ͬ����
�ĺ�������ͬ����![]() ���Ϊ
���Ϊ![]() ������
������![]() ���
���![]() �غ�ʱ
�غ�ʱ![]() ����
����![]() �����Ϊ
�����Ϊ![]() ������
������![]() ���
���![]() �غ�ʱ��
�غ�ʱ��![]() ������
������![]() ���۲�ͼ��
���۲�ͼ��![]() ʱ��д��
ʱ��д��![]() ��ȡֵ��Χ��������ڴ˷�Χ��
��ȡֵ��Χ��������ڴ˷�Χ��![]() �����ֵ��
�����ֵ��

���𰸡���1��![]() ��
��![]() ��
��![]() ����2��
����2��![]() ��
��![]() �����ɼ���������3��-2��x��2����
�����ɼ���������3��-2��x��2����![]() ʱ��
ʱ��![]() �����ֵΪ16��
�����ֵΪ16��
��������
��1����������![]() ��
��![]() �ɵ�
�ɵ�![]() ����
����![]() ��
��![]() ����
����![]() �����
�����![]() ��
��![]() ��
��
��2����ֱ��![]() �Ľ���ʽ��
�Ľ���ʽ��![]() ������
������![]() Ϊֱ�Ƕ��㣬
Ϊֱ�Ƕ��㣬![]() ��
��![]() ������
������![]() Ϊֱ�Ƕ��㣬
Ϊֱ�Ƕ��㣬![]() ��
��![]() ������
������![]() Ϊֱ�Ƕ��㣬��
Ϊֱ�Ƕ��㣬��![]() ���������⣻
���������⣻
��3����![]() ����
����![]() ����
����![]() ��
��![]() ����
����![]() ������ֱ��
������ֱ��![]() �Ľ���ʽ��
�Ľ���ʽ��![]() ����
����![]() ��
��![]() ���ƽ����
���ƽ����![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() �ڵ�
�ڵ�![]() ����֪
����֪![]() ��
��![]() ������
������![]() ����
����![]() ʱ��
ʱ��![]() �����ֵΪ
�����ֵΪ![]() .
.
��1����������![]() ��
��![]() �ɵ�
�ɵ�![]() ��
��
��![]() ����
����![]()
��![]() ��
��
���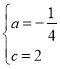 ��
��
��![]() ��
��
��![]() ��
��
��2����ֱ��![]() �Ľ���ʽ��
�Ľ���ʽ��![]() ��
��
����![]() Ϊֱ�Ƕ��㣬
Ϊֱ�Ƕ��㣬![]() ��
��
��![]() ��
��
ֱ��![]() ����ʽΪ
����ʽΪ![]()
����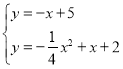 ��
��
���![]() ��
��![]() ��
��
��![]() ��
��
����![]() Ϊֱ�Ƕ��㣬
Ϊֱ�Ƕ��㣬![]() ��
��
ͬ����![]() ����ʽ��
����ʽ��![]() ��
��
����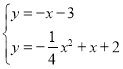 ��
��
���![]() ��
��![]() ��
��
��![]() ��
��
����![]() Ϊֱ�Ƕ��㣬��
Ϊֱ�Ƕ��㣬��![]()
��![]() ��
��![]() ��
��
�� ��
��
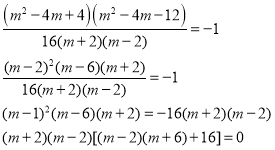
![]() ��
��![]() ���⣩
���⣩
���![]() ��
��![]() ��������������ȥ����
��������������ȥ����
���![]() ��
��![]() ��
��
��3����![]() ��
��
��![]() ��
��
��![]() ��
��![]() ����
����![]() ��
��
����ֱ��![]() �Ľ���ʽ��
�Ľ���ʽ��![]() ��
��
��![]() ��
��![]() ���ƽ����
���ƽ����![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��
![]()
![]()
��![]() ��
��![]() �ڵ�
�ڵ�![]() ����֪
����֪![]() ��
��
![]()
![]()
![]() ��
��
��![]() ʱ��
ʱ��![]() �����ֵΪ16��
�����ֵΪ16��

 Сѧѧϰ�ð���ϵ�д�
Сѧѧϰ�ð���ϵ�д� Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д�