题目内容
完成下面证明：
（1）如图1，已知直线b∥c，a⊥c，求证：a⊥b
证明：∵a⊥c （已知）
∴∠1= （垂直定义）
∵b∥c （已知）
∴∠1=∠2 （ ）
∴∠2=∠1=90° （ ）
∴a⊥b （ ）
（2）如图2：AB∥CD，∠B+∠D=180°，求证：CB∥DE
证明：∵AB∥CD （已知）
∴∠B= （ ）
∵∠B+∠D=180° （已知）
∴∠C+∠D=180° （ ）
∴CB∥DE （ ）
解答：
（1）证明：如图1，∵a⊥c（已知），
∴∠1=90°（垂直定义），
∵b∥c（已知），
∴∠1=∠2（两直线平行，同位角相等 ），
∴∠2=∠1=90°（等量代换 ），
∴a⊥b（垂直的定义 ）；
（2）证明：如图2，∵AB∥CD （已知），
∴∠B=∠C（两直线平行，内错角相等），
∵∠B+∠D=180°（已知），
∴∠C+∠D=180°（等量代换 ），
∴CB∥DE（同旁内角互补，两直线平行 ）．
故答案是：（1）∠2；两直线平行，同位角相等；等量代换；垂直的定义；
（2）∠C；两直线平行，内错角相等；等量代换；同旁内角互补，两直线平行．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
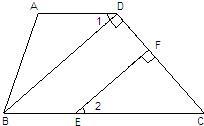19、如图，在四边形ABCD中，∠A=104°-∠2，∠ABC=76°+∠2，BD⊥CD于D，EF⊥CD于F．
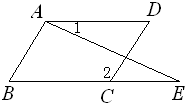25、学着说点理：完成下面证明，并注明理由
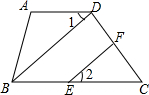如图，在四边形ABCD中，∠A=134°-∠2，∠ABC=46°+∠2，BD⊥CD于点D，EF⊥CD于点F．求证：∠1=∠2．请你完成下面证明过程．
