题目内容
【题目】![]() ,
,![]() 两地相距
两地相距![]() .甲、乙两人都由
.甲、乙两人都由![]() 地去
地去![]() 地,甲骑自行车,平均速度为
地,甲骑自行车,平均速度为![]() ;乙乘汽车,平均速度为
;乙乘汽车,平均速度为![]() ,且比甲晚
,且比甲晚![]() 出发.设甲的骑行时间为
出发.设甲的骑行时间为![]() .
.
(1)根据题意,填写下表:
时间 与 | 0.5 | 1.8 | ______ |
甲与 | 5 | ______ | 20 |
乙与 | 0 | 12 | ______ |
(2)设甲,乙两人与![]() 地的距离为
地的距离为![]() 和
和![]() ,写出
,写出![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)设甲,乙两人之间的距离为![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)2;18;20 (2)![]() ;
;![]() (3)1.2或1.6
(3)1.2或1.6
【解析】
解:(1)2,18,20;
【解法提示】由题意知:甲、乙二人平均速度分别为10 km/h和40 km/h,且乙比甲晚1.5h出发,当时间![]() 时,甲与A地的距离是
时,甲与A地的距离是![]() (km),
(km),
当甲与A地的距离20km时,甲的行驶时间是![]() (h),此时乙行驶的时间是
(h),此时乙行驶的时间是![]() (h),所以乙与A地的距离是
(h),所以乙与A地的距离是![]() (km).
(km).
(2)由题意知:![]() ,
,
当![]() 时,乙还没有出发,
时,乙还没有出发,
∴![]() ,
,
当![]() 时,设
时,设![]() 与x之间的函数解析式为
与x之间的函数解析式为![]() ,
,
将点![]() ,
,![]() 代入,
代入,
可得![]() ,
,
解得![]() ,
,
∴![]() .
.
综上可得:
![]() ;
;
(3)根据题意,
得![]() ,
,
当![]() 时,由
时,由![]() ,得
,得![]() ,
,
当![]() 时,由
时,由![]() ,得
,得![]() ,
,
∴当![]() 时,x的值是1.2或1.6
时,x的值是1.2或1.6

【题目】例 如图①,李老师设计了一个探究杠杆平衡条件的实验:在一个自制的类似天平的仪器的左边固定托盘![]() 中放置一个重物,在右边活动托盘
中放置一个重物,在右边活动托盘![]() (可左右移动)中放置一定质量的砝码,使得仪器左右平衡.改变活动托盘
(可左右移动)中放置一定质量的砝码,使得仪器左右平衡.改变活动托盘![]() 与点
与点![]() 的距离
的距离![]() ,观察活动托盘
,观察活动托盘![]() 中砝码的质量
中砝码的质量![]() 的变化情况.实验数据记录如表:
的变化情况.实验数据记录如表:
| 10 | 15 | 20 | 25 | 30 |
| 30 | 20 | 15 | 12 | 10 |
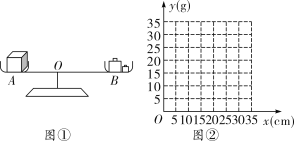
(1)把表中![]() 的各组对应值作为点的坐标,在图②的坐标系中描出相应的点,用平滑曲线连接这些点;
的各组对应值作为点的坐标,在图②的坐标系中描出相应的点,用平滑曲线连接这些点;
(2)观察所画的图象,猜测![]() 与
与![]() 之间的函数关系,求出函数关系式;
之间的函数关系,求出函数关系式;
(3)当砝码的质量为![]() 时,活动托盘
时,活动托盘![]() 与点
与点![]() 的距离是多少?
的距离是多少?
【题目】某种植基地种植一种蔬菜,它的成本是每千克2元,售价是每千克3元,年销量为10万千克.基地准备拿出一定的资金作绿色开发,若每年绿色开发投入的资金为![]() (万元),该种蔬菜的年销量将是原年销量的
(万元),该种蔬菜的年销量将是原年销量的![]() 倍,
倍,![]() 与
与![]() 的关系如下表:
的关系如下表:
| 0 | 1 | 2 | 3 | 4 | 5 | … |
| 1 | 1.5 | 1.8 | 1.9 | 1.8 | 1.5 | … |
(1)猜想![]() 与
与![]() 之间的函数类型是________函数,求出该函数的表达式并验证;
之间的函数类型是________函数,求出该函数的表达式并验证;
(2)求年利润![]() (万元)与绿色开发投入的资金
(万元)与绿色开发投入的资金![]() (万元)之间的函数关系式,当绿色开发投入的资金不低于3万元,又不超过5万元时,求此时年利润
(万元)之间的函数关系式,当绿色开发投入的资金不低于3万元,又不超过5万元时,求此时年利润![]() (万元)的最大值;
(万元)的最大值;
(注:年利润![]() 销售总额-成本费-绿色开发投入的资金)
销售总额-成本费-绿色开发投入的资金)
(3)若提高种植人员的奖金,发现又增加一部分年销量,经调查发现:再次增加的年销量![]() (万千克)与每年提高种植人员的奖金
(万千克)与每年提高种植人员的奖金![]() (万元)之间满足
(万元)之间满足![]() ,若基地将投入5万元用于绿色开发和提高种植人员的奖金,应怎样分配这笔资金才能使总年利润达到17万元且绿色开发投入大于奖金投入?(
,若基地将投入5万元用于绿色开发和提高种植人员的奖金,应怎样分配这笔资金才能使总年利润达到17万元且绿色开发投入大于奖金投入?(![]() )
)