题目内容
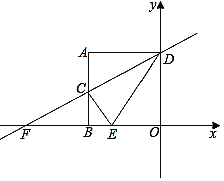
【题目】把两个直角三角形如图![]() 放置,使
放置,使![]() 与
与![]() 重合,
重合,![]() 与
与![]() 相交于点
相交于点![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 图
图![]() 中线段
中线段![]() 的长
的长![]() ________
________![]() ;
;![]() ________
________![]()
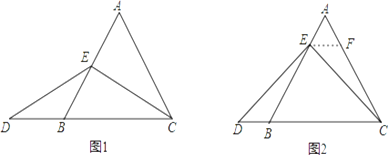
![]() 如图
如图![]() ,把
,把![]() 绕着点
绕着点![]() 逆时针旋转
逆时针旋转![]() 度
度![]() 得
得![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,若
,若![]() 恰好是以
恰好是以![]() 为底边的等腰三角形,求线段
为底边的等腰三角形,求线段![]() 的长.
的长.

【答案】(1)![]() ;
;![]() ;(2)
;(2)![]() .
.
【解析】
(1)过点O作OM⊥DC于点M,作ON⊥CB于点N,进而得出AD的长,再利用锐角三角函数关系得出DO的长,再利用勾股定理得出AO的长;
(2)利用旋转的性质以及锐角三角函数关系得出tan∠BCE1=tanα=![]() ,再利用tan∠D1CA=tanα=
,再利用tan∠D1CA=tanα=![]() ,即可得出FG的长,进而得出AF的长.
,即可得出FG的长,进而得出AF的长.
(1)过点O作OM⊥DC于点M,作ON⊥CB于点N,
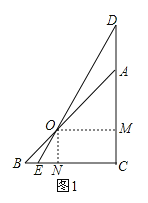
∵∠BAC=45°,AB=6![]() cm,
cm,
∴BC=AC=6cm,
∵CE=5cm,CD=10cm,
∴BE=1cm,AD=4cm,
设MO=xcm,
∴AM=xcm,
∴tanD=![]() ,
,
解得:x=4,
∴DM=8cm,MO=4cm,
∴DO=4![]() cm,
cm,
∵MO=AM=4cm,
∴AO=4![]() cm,
cm,
故答案为![]() ;
;![]() ;
;
![]() 作
作![]() 于
于![]() 点,
点,

设旋转角度为![]() 度,
度,
即![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
所以![]() ,
,
因为![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以![]() ,
,
∴![]() ,
,
解得:![]() ,
,
所以![]() .
.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目