Question

【题目】如图，四边形ABCD是边长为1的正方形，且DE＝，△ABF是△ADE的旋转图形

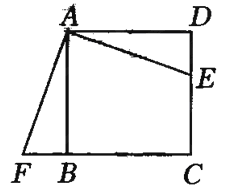
（1）旋转中心是哪一点？

（2）旋转了多少度？

（3）AF的长度是多少？

（4）如果连结EF，那么△AEF是怎样的三角形？

Answer 1

【答案】（1）旋转中心是点A；（2）顺时针旋转90°；（3）．（4）等腰直角三角形．

【解析】试题（1）、（2）观察图形，由△ADE到△ABF，可得出旋转中心，旋转角；

（3）根据对应边AE=AF，FB=DE=，在Rt△ABF中，使用勾股定理计算AF；

（4）根据旋转的性质，得到三角形中的边、角之间的关系，进行判断．

试题解析：观察图形，由△ADE到△ABF的旋转可知：

（1）旋转中心是点A；

（2）顺时针旋转90°；

（3）由旋转可知BF=DE=．

由勾股定理得：AF=．

（4）等腰直角三角形．

由旋转可知；AE与AF是对应边，

∴AE=AF，∠EAF=90°，

则△AEF是等腰直角三角形．