Question

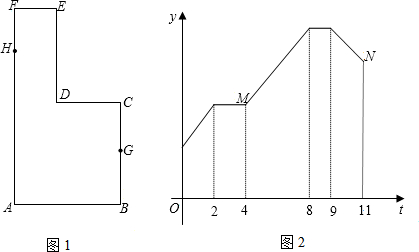
已知动点P以每秒2cm的速度沿如图所示的边框按从B→C→D→E→F→A的路径移动，相应的△ABP的面积S关于时间t的函数图象如图所示，若AB=6cm，则a=

24

，b=

17

．

Answer 1

分析：根据图甲得到当P在BC上时，以AB为底的高在不断增大，到达点C时，开始不变，根据图乙得到P在BC上移动了4秒，求出BC的长，在CD上移动了2秒，求出CD的长，在DE上移动了3秒，求出DE的长，根据AB-CD求出EF的长，由BC+DE求出AF的长，进而求出所需的时间，由图乙得到a是点P运行4秒时△ABP的面积，求出△ABP的面积确定出a的值，求出走完全程所有的时间即可确定出b的值．

解答：解：易知当P在BC上时，以AB为底的高在不断增大，到达点C时，开始不变，
由图乙得，P在BC上移动了4秒，那么BC=4×2=8cm；
在CD上移动了2秒，CD=2×2=4cm，
在DE上移动了3秒，DE=3×2=6cm，
∵AB=6cm，
∴EF=AB-CD=2cm，需要移动2÷2=1秒；AF=CB+DE=14cm．需要移动14÷2=7秒，
由图乙得，a是点P运行4秒时△ABP的面积，
∴S_△ABP=

1

2

×6×8=24，b为点P走完全程的时间为：t=9+1+7=17（秒），即b=17．
故答案为：24；17

点评：此题属于动点问题的函数图象，利用了数形结合的思想，弄清题意是解本题的关键．