��Ŀ����
����Ŀ����ͼ����֪�����ϵ�![]() ��ʾ����Ϊ
��ʾ����Ϊ![]() ����
����![]() ��ʾ����Ϊ
��ʾ����Ϊ![]() ��
��![]() ��������һ�㣬��
��������һ�㣬��![]() ������
������![]() �ӵ�
�ӵ�![]() ��������ÿ��
��������ÿ��![]() ����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊ
����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊ![]() �룮
�룮
��1�������ϵ�![]() ��ʾ����Ϊ �����ú�
��ʾ����Ϊ �����ú�![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��![]() ����ʾ����Ϊ ��
����ʾ����Ϊ ��
��2����![]() ��
��![]() ���е㣬
���е㣬![]() ��
��![]() ���е㣬��
���е㣬��![]() ���˶������У��߶�
���˶������У��߶�![]() �ij����Ƿ����仯�����仯����˵�����ɣ������䣬���߶�
�ij����Ƿ����仯�����仯����˵�����ɣ������䣬���߶�![]() �ij��ȣ�
�ij��ȣ�
��3������![]() �ӵ�
�ӵ�![]() ��������ÿ��
��������ÿ��![]() ����λ���ȵ��ٶ����������������˶�������
����λ���ȵ��ٶ����������������˶�������![]() �ӵ�
�ӵ�![]() �������Ե�ÿ��
�������Ե�ÿ������λ�������������������˶�����
![]() ����ͬʱ���������˶������У�
����ͬʱ���������˶������У�![]() ��
��![]() �ľ��룬
�ľ��룬![]() ��
��![]() �����У��Ƿ���������ξ�����ȵ�ʱ�����У��������ʱ��ֵ����û�У���˵�����ɣ�
�����У��Ƿ���������ξ�����ȵ�ʱ�����У��������ʱ��ֵ����û�У���˵�����ɣ�
���𰸡���1����![]() ��ʾ����Ϊ
��ʾ����Ϊ![]() ��
��![]() ����2���߶�
����2���߶�![]() �ij��Ȳ������仯����ֵΪ
�ij��Ȳ������仯����ֵΪ![]() ����3������������
����3������������![]() ��
��![]() ��
��![]() �룮
�룮
��������
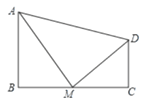
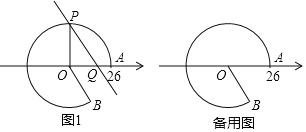
��1����C���ʾ����Ϊ![]() �����������������ľ��빫ʽ�������������⣬�ٸ��������ϵ���˶��Ϳ������P������ꣻ
�����������������ľ��빫ʽ�������������⣬�ٸ��������ϵ���˶��Ϳ������P������ꣻ
��2���������ۣ��ٵ���P�ڵ�A��C����֮���˶�ʱ���ڵ���P�˶�����C�����ʱ�������е�Ķ�����߶εĺͲ������MN��
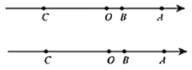
��3���ò�����ʾ��P��ʾ����Ϊ��![]() ����R��ʾ����Ϊ��
����R��ʾ����Ϊ��![]() ����Q��ʾ����Ϊ��
����Q��ʾ����Ϊ��![]() ����������빫ʽ�г����̿���⣮
����������빫ʽ�г����̿���⣮
��1�����![]() ��ʾ����Ϊ
��ʾ����Ϊ![]() �������⣬�ã�
�������⣬�ã�
![]() �����
�����![]()
�ʵ�![]() ��ʾ����Ϊ
��ʾ����Ϊ![]() ����
����![]() �ӵ�
�ӵ�![]() ���������˶����ٶ�Ϊ
���������˶����ٶ�Ϊ![]() ������
������![]() ��
��
��2���߶�![]() �ij��Ȳ������仯
�ij��Ȳ������仯
���ɣ������������
�ٵ���![]() ��
��![]() ����֮���˶�ʱ����ͼ��
����֮���˶�ʱ����ͼ��

![]() ��
��
�ڵ���![]() �˶�����
�˶�����![]() �����ʱ����ͼ��
�����ʱ����ͼ��

![]() ��
��
�����������߶�![]() �ij��Ȳ������仯����ֵΪ
�ij��Ȳ������仯����ֵΪ![]() ��
��
��3������Ŀ�ɵã��������ʱ��Ϊ![]() �룬ʹ��
�룬ʹ��![]() ��
��![]() ���룬
���룬![]() ��
��![]() ������ȣ�����ʱ���������������ʾΪ��
������ȣ�����ʱ���������������ʾΪ��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ���룬
���룬![]() ��
��![]() ������ȣ���
������ȣ���![]() ��ʱ��
��ʱ��
![]()
![]()
![]() ��
��
��![]() ��
��
��ã�![]() ���룩
���룩
��![]() ��
��
��ã�![]() ���룩
���룩
����������![]() ��
��![]() ��
��![]() �룮
�룮

����Ŀ��ijУҪ��С�졢С����С������ͬѧ����ѡһ��ͬѧ�μ���ѧ������������������Ĵ�ר������У��������˵ijɼ����±���ʾ��
ѧ�� ר�� | ����֤�� | PISA���� | Ӧ���� | �������� |
�� | 70 | 75 | 80 | 85 |
�� | 80 | 80 | 72 | 76 |
�� | 75 | 75 | 90 | 65 |
��1�������С���ƽ����Ϊ���٣�
��2����У�����Ĵ�ר�⿼�Գɼ�����Ҫ�̶Ȳ�ͬ������ÿ��ר��ɼ�һ��Ȩ�أ�Ȩ�ر�����Ϊx��1��2��1�����ó����˵ijɼ�����Ȩƽ�����������Ӹ߷ֵ��ͷ�����ΪС����С����С�죬��������x��ֵ��
����Ŀ��ij�н���չ�����߽��й���ѧʷ��Ϊ�����֪ʶ�������������ѧУ�Ա�У100���μ�ѡ������ͬѧ�ijɼ���A��B��C��D�ĸ��ȼ�����ͳ�ƣ����Ƴ����²�������ͳ�Ʊ�������ͳ��ͼ��
�ɼ��ȼ� | Ƶ���������� | Ƶ�� |
A | 4 | 0.04 |
B | m | 0.51 |
C | n | |
D | ||
�ϼ� | 100 | 1 |
��1����m=�� ����n=�� ����
��2��������ͳ��ͼ�У�����C�ȼ�������Ӧ�ĽǵĶ�����
��3���ɼ��ȼ�ΪA��4��ͬѧ����1��������3��Ů�����ִ��������ѡ2��ͬѧ����ѧУ�μ�ȫ�б�����������״ͼ�������б������ǡ��ѡ����1��1Ů���ĸ��ʣ�