题目内容
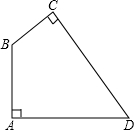 四边形ABCD中,∠A=∠C=90°,∠ADC=60°,AB=11,BC=2,则BD=________.
四边形ABCD中,∠A=∠C=90°,∠ADC=60°,AB=11,BC=2,则BD=________.
14
分析:延长AB与DC的延长线相交于点E,构造了两个30°的直角三角形,首先在直角三角形CBE中求得BE的长,再进一步在直角三角形ADE中,求得AD的长,再在直角三角形BAD中由勾股定理求得BD.
解答:如图,延长AB与DC的延长线相交于点E.
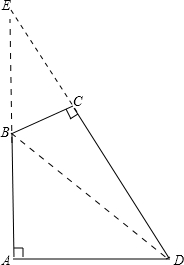
在Rt△ADE中,∵∠ADE=60°,
∴∠E=30°.
在Rt△BCE中,sinE= ,
,
∴BE= =4,
=4,
∴AE=AB+BE=11+4=15.
在Rt△DAE中,tanE= ,
,
∴AD=AE•tanE=15× =5
=5 ,
,
在Rt△BAD中,
BD=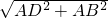 =
=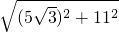 =14,
=14,
故答案为:14.
点评:此题考查的知识点是解直角三角形,关键要特别注意构造30°的直角三角形,熟练运用锐角三角函数求解.
分析:延长AB与DC的延长线相交于点E,构造了两个30°的直角三角形,首先在直角三角形CBE中求得BE的长,再进一步在直角三角形ADE中,求得AD的长,再在直角三角形BAD中由勾股定理求得BD.
解答:如图,延长AB与DC的延长线相交于点E.

在Rt△ADE中,∵∠ADE=60°,
∴∠E=30°.
在Rt△BCE中,sinE=
 ,
,∴BE=
 =4,
=4,∴AE=AB+BE=11+4=15.
在Rt△DAE中,tanE=
 ,
,∴AD=AE•tanE=15×
 =5
=5 ,
,在Rt△BAD中,
BD=
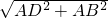 =
=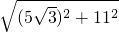 =14,
=14,故答案为:14.
点评:此题考查的知识点是解直角三角形,关键要特别注意构造30°的直角三角形,熟练运用锐角三角函数求解.

练习册系列答案
相关题目
 23、如图,四边形ABCD中,对角线AC、BD相交于点E.已知:DA=DC,E为AC中点.
23、如图,四边形ABCD中,对角线AC、BD相交于点E.已知:DA=DC,E为AC中点.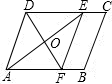 如图所示,在平行四边形ABCD中,AE是∠DAB的平分线,EF∥AD交AB于点F,若AB=9,CE=4,AE=8,则DF等于( )
如图所示,在平行四边形ABCD中,AE是∠DAB的平分线,EF∥AD交AB于点F,若AB=9,CE=4,AE=8,则DF等于( ) 17、如图,在平行四边形ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AB、CD于E、F.请写出图中三对全等的三角形:
17、如图,在平行四边形ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AB、CD于E、F.请写出图中三对全等的三角形: 7、如图,在四边形ABCD中,AD=CB,∠ACB=∠CAD.求证:AB=CD.
7、如图,在四边形ABCD中,AD=CB,∠ACB=∠CAD.求证:AB=CD.