题目内容
求方程
的实数根．
解：方程可变形为：
x2+2xy+y2+3x2-y-4
+4=0，
∴（x+y）2+
=0，
∵（x+y）2≥0，≥0，
∴
，
解得：
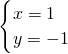或
，
经检验，均为原方程的解．
∴原方程的根为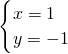：或．
分析：本题是已知一个方程，但要求出两个未知数的值，而要确定两个未知数的值，一般需要两个方程．因此，要将已知方程变形，看能否出现新的形式，以利于解题．
点评：本题考查了无理方程及解二元一次方程组，难度不大，掌握应用非负数的性质“几个非负数之和为零，则这几个非负数都为零”，可将一个等式转化为几个等式，从而增加了求解的条件．
可变形为：x2+2xy+y2+3x2-y-4
+4=0，∴（x+y）2+
=0，∵（x+y）2≥0，
≥0，∴
，解得：
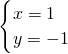或，经检验，均为原方程的解．
∴原方程的根为：
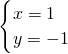或．分析：本题是已知一个方程，但要求出两个未知数的值，而要确定两个未知数的值，一般需要两个方程．因此，要将已知方程变形，看能否出现新的形式，以利于解题．
点评：本题考查了无理方程及解二元一次方程组，难度不大，掌握应用非负数的性质“几个非负数之和为零，则这几个非负数都为零”，可将一个等式转化为几个等式，从而增加了求解的条件．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目