题目内容
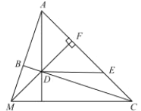
【题目】如图,点A是双曲线y=![]() (x>0)上的一点,连结OA,在线段OA上取一点B,作BC⊥x轴于点C,以BC的中点为对称中心,作点O的中心对称点O′,当O′落在这条双曲线上时,
(x>0)上的一点,连结OA,在线段OA上取一点B,作BC⊥x轴于点C,以BC的中点为对称中心,作点O的中心对称点O′,当O′落在这条双曲线上时,![]() =________.
=________.

【答案】![]()
【解析】
过点A作AD⊥x轴于点D,由点A在反比例函数图象上设出点A的坐标,由O、A点的坐标即可得出直线OA的解析式,设出点B的坐标,由中点坐标公式以及中心对称的性质找出点O′的坐标,根据反比例函数图象上点的坐标特征即可得出点B、A横坐标之间的关系,由此即可得出结论.
过点A作AD⊥x轴于点D,如图所示.

∵点A在反比例函数y=![]() 的图象上,
的图象上,
∴设点A的坐标为(m,![]() ),
),
∴直线OA的解析式为y=![]() x,
x,
设点B的坐标为(n,![]() ),则点C的坐标为(n,0),
),则点C的坐标为(n,0),
线段BC中点的坐标为(n,![]() ).
).
∵点O、O′关于点(n,![]() )对称,
)对称,
∴点O′的坐标为(2n,![]() ).
).
∵点O′在反比例函数y=![]() 的图象上,
的图象上,
∴2n![]() =k,即
=k,即![]() ,
,
∴![]() .
.
∵BC⊥x轴,AD⊥x轴,
∴BC∥AD,
∴![]() =
=![]() .
.
故答案为:![]() .
.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
【题目】八(2)班分成甲、乙两组进行一分钟投篮测试,并规定得6分及以上为合格,得9分及以上为优秀,现两组学生的一次测试成绩统计如下表:
成绩(分) | 4 | 5 | 6 | 7 | 8 | 9 |
甲组人数(人) | 1 | 2 | 5 | 2 | 1 | 4 |
乙组人数(人) | 1 | 1 | 4 | 5 | 2 | 2 |
(1)请你根据上表数据,把下面的统计表补充完整,并写出求甲组平均分的过程;
统计量 | 平均分 | 方差 | 众数 | 中位数 | 合格率 | 优秀率 |
甲组 |
| 2.56 |
| 6 | 80.0% | 26.7% |
乙组 | 6.8 | 1.76 | 7 |
| 86.7% | 13.3% |
(2)如果从投篮的稳定性角度进行评价,你认为哪组成绩更好?并说明理由;
(3)小聪认为甲组成绩好于乙组,请你说出支持小聪观点的理由;