Question

已知A、B、C、D是圆O上的四点，弧CD＝弧BD，AC是四边形ABCD的对角线，（1）如图，连接BD，若∠CDB＝60°，求证：AC是∠DAB的平分线；

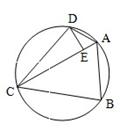
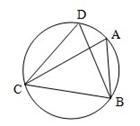   （2）如图，过点D作DE⊥AC，垂足为E，若AC＝7，AB＝5，求线段AE的长度.

Answer 1

（1）证明：∵ ＝，

     ∴ CD＝BD.        

     又∵∠CDB＝60°，

     ∴△CDB是等边三角形. 

     ∴ ∠CDB＝∠DBC.    

    ∴   ＝.

∴ ∠DAC＝∠CAB.

∴ AC是∠DAB的平分线.    

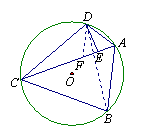
（2）解法一：连结DB.      

在线段CE上取点F，使EF＝AE，连结DF.   

∵ DE⊥AC，

∴ DF＝DA，∠DFE＝∠DAE.    

∵ ＝，

∴ CD＝BD.

∴∠DAC＝∠DCB.

∴ ∠DFE＝∠DCB.  

∵ 四边形ABCD是圆内接四边形，

∴ ∠DAB＋∠DCB＝180°.

又∵∠DFC＋∠DFE＝180°，

∴ ∠DFC＝∠DAB

∵∠DCA＝∠ABD，

∴△CDF≌△BDA.  

∴CF＝AB.      

∵AC＝7， AB＝5，

∴ AE＝1.      

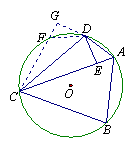
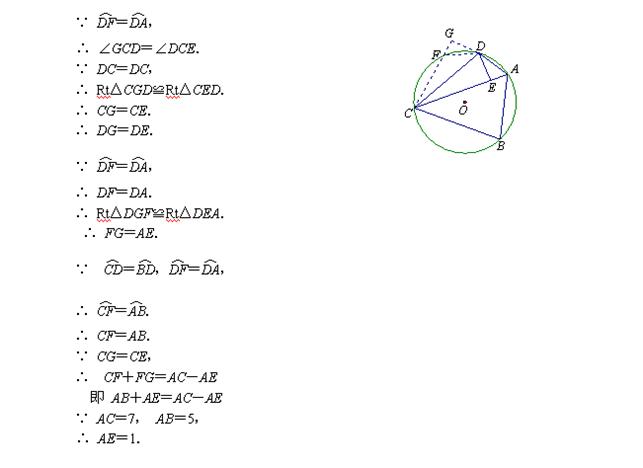
解法二：在上取一点F，使得＝ ，

     连结CF，延长CF，过D作DG⊥CF，垂足为G.